algorigram

C1-ALGO-02 : Des algorithmes aux algorigrammes#

Objectifs pédagogiques#

  • déchiffrer un algorigramme et en déduire l’algorithme

  • dessiner un algorigramme à partir d’un algorithme simple

Doit-on être bon en maths pour être bon en algorithmique (et en programmation) ?#

NON.

Et encore NON !

Les compétences requises pour faire de l’algorithmique sont :

  1. Savoir expliquer : comment arriver à un résultat sans la moindre ambigüité

  2. Savoir formaliser son raisonnement

  3. Utiliser un langage simple (qu’il soit visuel, en langue française ou dans une autre langue, ou mathématique)

  4. Savoir concevoir et écrire (ou dessiner) la séquence d’instructions qui décrit comment résoudre le problème

Exercice 1 : construire des algorigrammes#

Voici quelques exemples d’algorithmes. Ecrivez l’algorigramme correspondant

Demande de rançon#

rancon

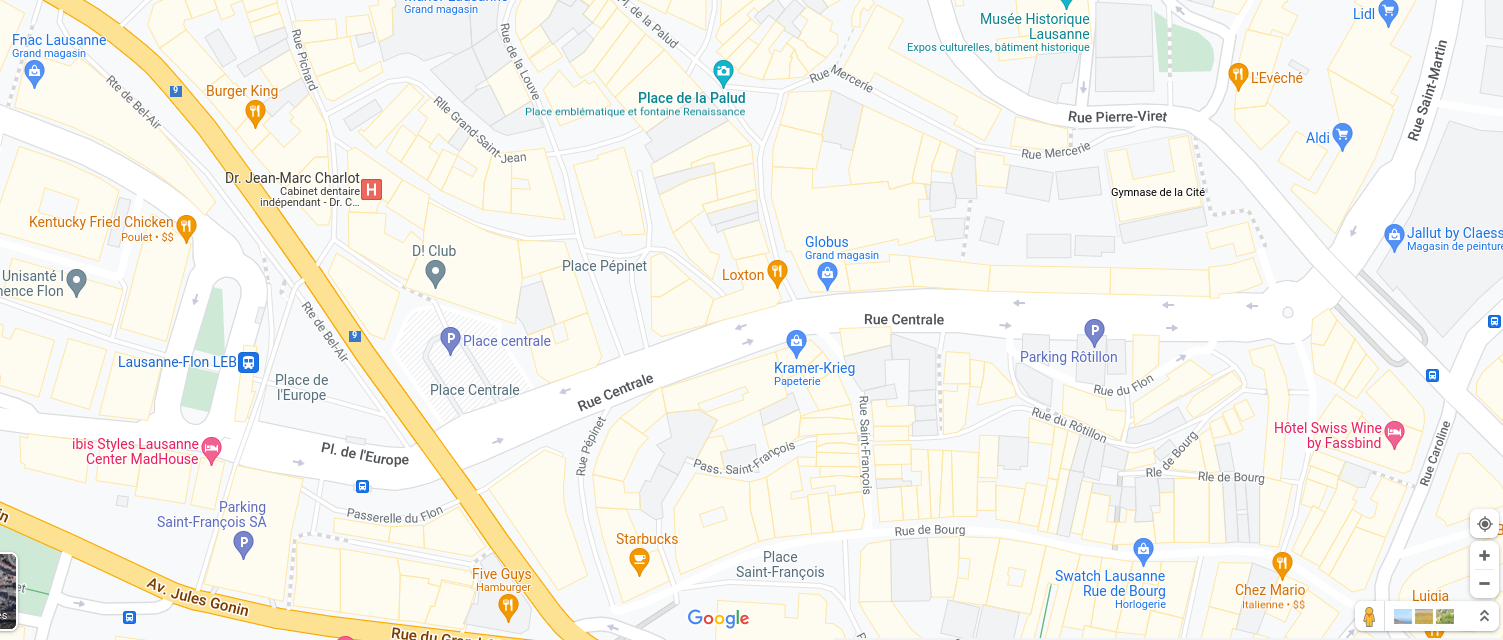
Donner son chemin à un touriste#

Comment expliquer à un touriste de passage comment aller de la Place Saint-François à la Cathédrale de Lausanne ?

carte

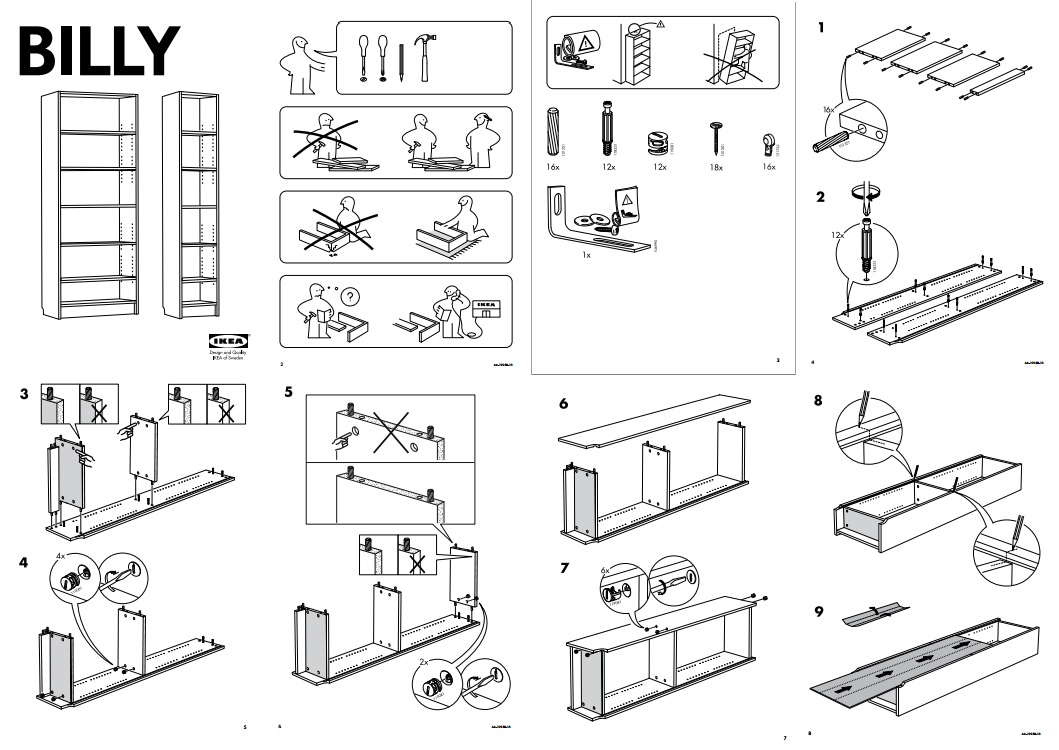
Monter un meuble IKEA#

Quelles sont les étapes pour construire la célèbre étagère Billy du géeant suédois ?

IKEA

Exercice 2 (plus difficile)#

Vous avez emprunté 100 CHF à une amie. Celle-ci vous demande de vous rembourser 10 CHF par mois jusqu’à extinction de la dette. Dessinez l’algorigramme

Exercice 3 (encore plus difficile)#

Reprenez la donnée de l’exercice 2. L’emprunt à votre amie n’est plus de 100 CHF, ni de 10 CHF de remboursement par mois, mais doit pouvoir être précisé à l’entrée de l’algorithme.

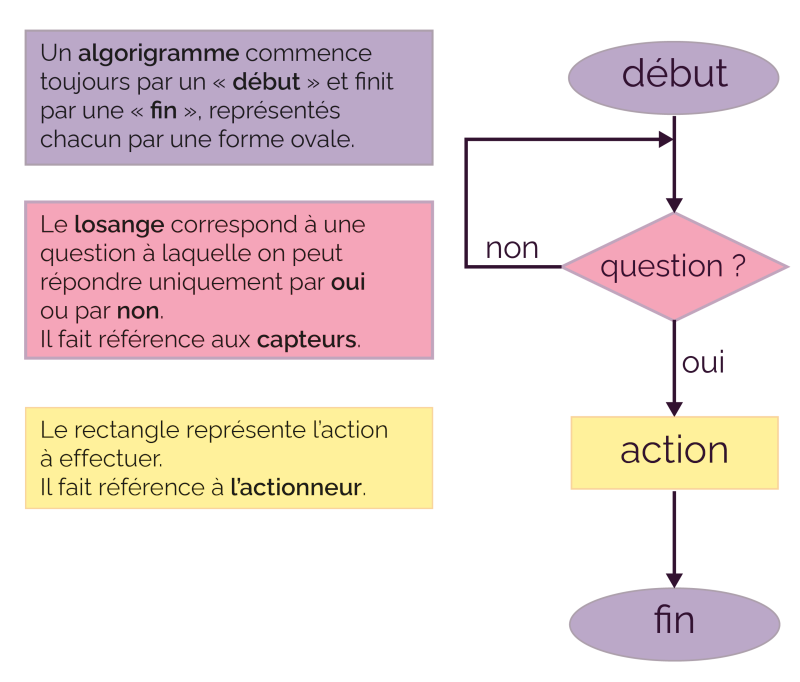
Les 4 briques des algorithmes#

Tous les algorithmes existants sont basés sur 4 briques :

  1. La lecture et l’écriture (communication entre l’utilisateur et l’algorithme)

  2. L’affectation de variables

  3. Les tests

  4. Les boucles

Définition : algorithme récursif#

Un algorithme récursif est un algorithme qui fait appel à lui-même. En d’autres termes, l’algorithme résoud un problème en calculant des problèmes plus petits du même problème.

Exercice 5 (un peu de maths)#

Dessinez l’algorigramme qui calcule la suite de Fibonacci définie par :

  1. \(Fib_0 = 0\)

  2. \(Fib_1 = 1\)

  3. \(Fib_n = F_{n-1} + Fib_{n-2}\)

fibo

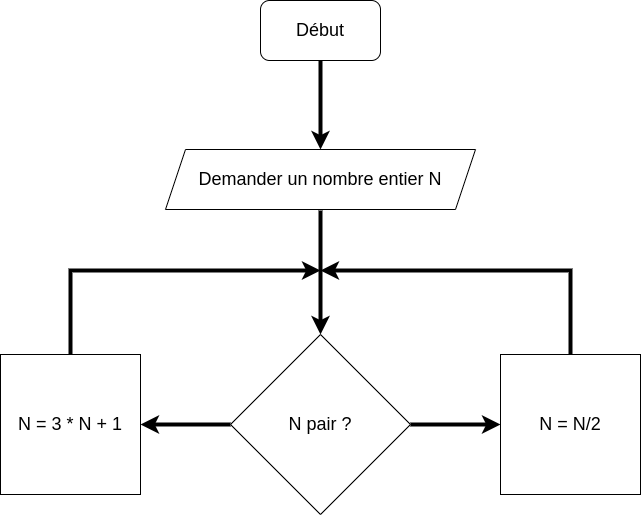
Conjecture de Syracuse#

En mathématiques, une conjecture est un énoncé dont il n’existe pas de démonstration. Celle de Syracuse a fait beaucoup parler d’elle tant elle est simplissime dans sa formulation mais que personne n’a pu la démontrer depuis sa formulation en 1928.

La conjecture de Syracuse fait appel à la récursivité.

La conjecture se définit ainsi :

  1. ENTREE : n

  2. SI n est PAIR, alors n = n / 2

  3. SINON n = 3 * n + 1

  4. La suite se termine lorsqu’on a atteint n == 1 et boucle sur la suite (1,4,2,1,4,2,…)

syracuse