
C2-ALGO-05 : Théorie des graphes, le voyageur de commerce#
Objectifs pédagogiques#
connaître le problème du voyageur de commerce (TSP)
appliquer un algorithme glouton sur un graphe exemple du TSP
Le problème du Voyageur de commerce#
Le problème du voyageur de commerce, ou traveling salesman problem (TSP) peut se définir ainsi pour les états-unis :
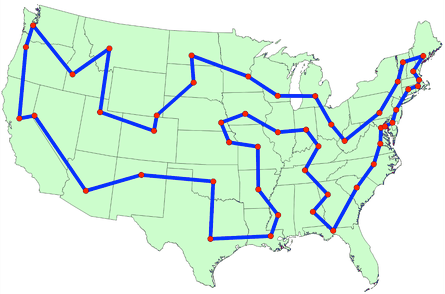
Le problème du voyageur de commerce se définit de la façon suivante. Etant donné un ensemble de villes, un voyageur de commerce (ou un commis voyageur) doit trouver le chemin le plus court passant par toutes les villes une seule fois.
En terme de graphes, chaque ville est un sommet du graphe, chaque arête étant un chemin entre deux villes. Le graphe n’est pas forcément totalement connecté, c’est-à-dire que tous les sommets sont reliés à tous les sommets.
Complexité du problème#
Il n’existe aucun algorithme qui permet de résoudre le TSP sans calculer toutes les solutions possibles. C’est donc un problème très difficile dont la complexité est \(\mathcal O (N!)\)
Exemple sur le graphe des états-unis#
Sur la carte des états-unis continentaux (Mainland en anglais), c’est-à-dire les états encadrés à l’est par l’Océan Atlantique, le golfe du Mexique au sud-est, l’Océan Pacifique à l’ouest et le Canada au Nord, il y a 48 états. Les 2 restants sont les Îles Hawaï et l’Alaska.
Données :
\(48\) sommets complètement reliés (routes, trains, avions)
Nombre de chemins possibles : \(48 ! = 12413915592536072670862289047373375038521486354677760000000000\), soit \(1.2 * 10^{61}\)
Par hypothèse, imaginons qu’un ordinateur soit capable de calculer \(10^9\) soit un milliard de chemins par seconde et que nous mettions tous les ordinateurs de la planète sur le calcul du voyageur de commerce sur les 48 capitales des états américains. On estime le nombre total d’ordinateurs dans le monde entre \(5\) et \(10\) milliards. Prenons la valeur supérieure soit \(10^{10}\) (10 milliards)
\(10^9\) milliards de chemins par seconde
\(31536000\) secondes par année, donc \(3.1 * 10^{17}\) chemins calculé par ordinateur chaque année
\(10^{10}\) ordinateurs dans le monde (en 2023)
\(3.1 * 10^{27}\) chemins calculés chaque année par tous les ordinateurs de la planète
Tous les chemins seront calculés après \(10^{44}\) années
L’âge de l’Univers est estimé à \(1.4 * 10^{10}\) (14 milliards d’années)
Exercice 1 : Le voyageur de commerce (TSP)#
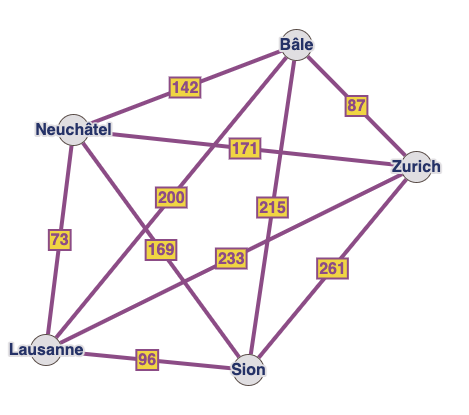
Depuis Lausanne, quel est le meilleur itinéraire qui passe par : Neuchâtel, Bâle, Zürich et Sion ?
Algorithme glouton : “Greedy algorithms”#
Un algorithme glouton est un algorothme qui choisi :
Appliquer une solution localement valable
Mesurer le résultat
il permet d’approcher une solution à un problème complexe mais pas de trouver la solution optimale
Changer d’approche#
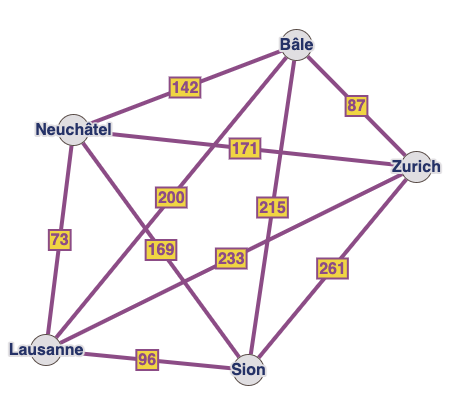
Proposition : prendre le prochain plus court chemin vers une ville non visitée
Lausanne-Neuchâtel-Bâle-Zurich-Sion-Lausanne = 659km
C’est bien ?
Accessoirement ce chemin emprunte les 4 chemins les plus courts possibles entre 2 villes…
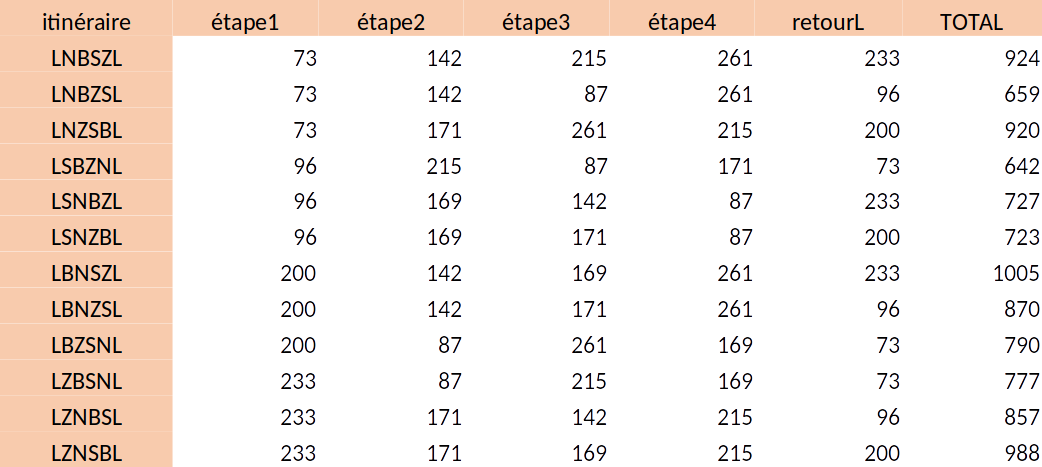
Gagnant improbable
Lausanne-Sion
Sion-Bâle
Bâle-Zurich
Zurich-Neuchâtel
Neuchâtel-Lausanne
Est-ce une bonne solution ?
2e meilleur
17km de plus que le meilleur
346 de moins que le pire !
En fait, oui c’est pas mal, mais c’était pas évident de le savoir
Exercice 2 : Simulateur TSP online#
Vous pouvez simuler le TSP sur le site suivant

Comment procéder ?#
Voici la matrice d’adjacence :
Lausanne
Nauchâtel
Zürich
Sion
Bâle
Lausanne
0
73
233
96
200
Neuchâtel
73
0
171
169
142
Zürich
233
171
0
261
87
Sion
96
169
261
0
215
Bâle
200
142
87
215
0
Si on calcule tous les itinéraires possibles :
Avec
4candidates comme première étape,3comme seconde,2comme troisième et une dernière : \(4! = 24\) possibilitésMais tout est à double : donc
12Avec
12villes : \(\frac{12 !}{2} = 239500800\) : 240 millions !Complexité du TSP : \(\mathcal O (N!)\)
Pas d’autre solution