TP2-STRAT-01 : Gestion des erreurs et Monte-Carlo

Objectifs pédagogiques

• Connaître une nouvelle classe d’algorithmes : les méthodes de Monte-Carlo

• Comprendre un code informatique écrit par quelqu’un d’autre

• Corriger un code informatique en analysant les erreurs de types algorithmique, programmatique et syntaxique

Méthodes de Monte-Carlo

La classe d’algorithmes dont font partie les méthodes de Monte-Carlo sont une classe d’algorithmes probabilistes et statistiques. Elle font intervenir les nombres aléatoires. On les utilise dans la résolution de problèmes très difficiles dont il est souvent impossible de trouver une solution. Citons par exemple :

• de problème du voyageur de commerce (TSP)

• des problèmes en physique des particules

• le problème du risque dans une décision financière

Elles tirent leur nom du célèbre Casino de Monte-Carlo à Monaco.

Historique

La classe d’algorithmes Monte-Carlo est née dans le cadre du Projet Manhattan (développement de la première bombe atomique américaine pendant la seconde guerre mondiale). On en attribue la paternité à Stanisław Ulam, un collègue de John Von Neuman,

Fonctionnement de l’algorithme

Les méthodes de Monte-Carlo (ou algorithme de Monte-Carlo) est une méthode visant à calculer une valeur numérique en utilisant des procédés aléatoires, c’est-à-dire des techniques probabilistes.

Sur la base de la connaissance des propriétés de ces valeurs numériques, il s’agit de tirer des nombres aléatoires et vérifier qu’ils remplissent ces propriétés. Deux cas se présentent :

1. Le nombre aléatoire remplit ces propriétés, alors on le conserve

2. Le nombre aléatoire ne remplit pas ces propriétés, on le supprime.

Finalement, avec un très grand nombre de tirs de nombres aléatoires, il est possible de calculer un ratio (un rapport) entre le nombre de tirs conservés et le nombre de tirs global afin d’obtenir une approximation de la valeur numérique recherchée.

Exercice 1

Problème : Estimation de \( \pi \) en utilisant la méthode de Monte-Carlo.

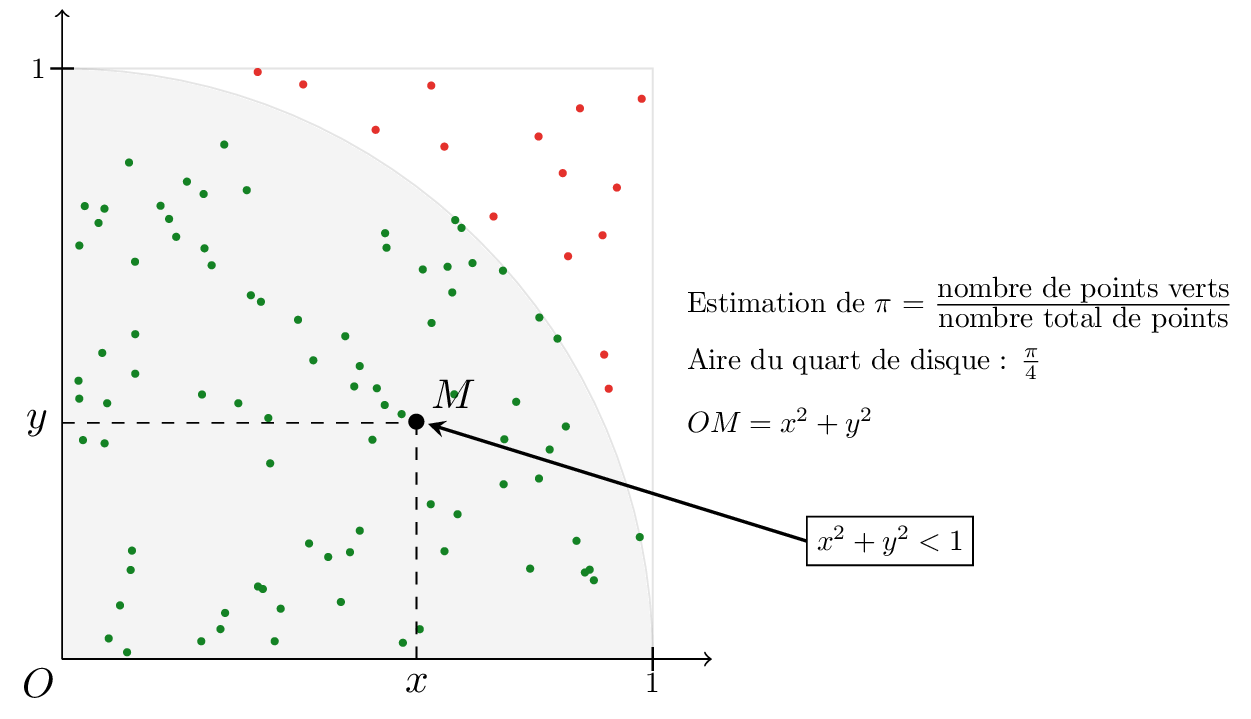
(source)

Voici un code qui implémente l’algorithme de Monte-Carlo pour approximer \( \pi \)

Identifiez toutes les erreurs et donnez le type d’erreur (syntaxe, programme, algorithme). Corrigez le code.

import randomm
nb_exp = 10000
succes == 0
for i in range(nb_exp):
    x = random.random()
   y = random.random()
    if x * x + y * y <= 1:
        succes = succes + 1
nb_succes = 4 * succes / nb_exp
print(nb_succes)

Exercice 2

Voici un algorigramme qui contient des erreurs. Identifiez-les avec leur type.

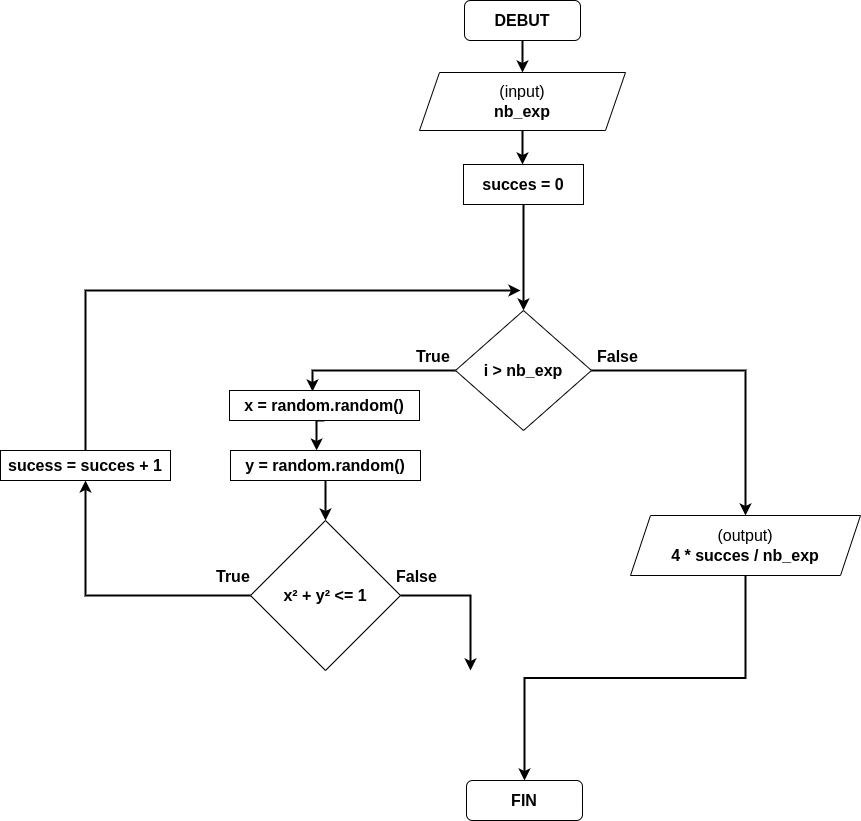
Exercice 3 : lancement d’un dé à jouer

Lorsqu’on lance un dé, on a \(\frac{1}{6}\) chance de tirer n’importe quel numéro entre 1 et 6, soit 16.66 %.

Utilisez un algorithme Monte-Carlo pour simuler le lancement d’un dé et approximer les probabilités pour chaque nombre.

Exercice 4 (pour aller plus loin) : Somme de deux dés à jouer

Beaucoup de jeux de stratégie, de rôle ou de hasard demandent de tirer deux dés et de calculer la somme des deux dés. La probabilité de chaque combinaison est identique : c’est le hasard. Par contre il existe, pour chaque somme possible (de 2 à 12), une ou plusieurs combinaisons possibles et donc des probabilités différentes.

Dans cet exercice, nous allons simuler cette somme pour approximer les probabilités de chaque combinaison.

Exercice 4.1 : les combinaisons et leurs probabilités

Sur une feuille de papier, écrivez toutes les combinaisons possibles du jet de deux dés. Il y en a 36 au total avec les permutations possibles. Complétez le tableau suivant :

Somme	Combinaisons possibles	probabilité
2	+	\(\frac{1}{36}\) soit 2.77 %
3	+ et +	\(\frac{2}{36}\) soit 5.55 %
4	+ et + et +	\(\frac{3}{6}\) soit 8.33 %
5
6
7
8
9
10
11
12

Exercice 4.2 : Simulation Monte-Carlo en Python

• Ecrivez un programme qui simule la somme de deux dés lancés. L’entrée de l’algorithme est le nombre d’expériences (nbExps). Vous devez utiliser la fonction du module random.randint(1,6) pour tirer des nombres aléatoires entre 1 et 6.

• Modifiez la valeur du nombre d’expériences pour affiner vos prédictions.

• Comparez les approximations avec les calculs formels de l’exercice 4.1.

Exercice 5 (pour aller vraiment plus loin) : Roulette française

Le jeu de la roulette au casino est un jeu de hasard consistant en en appareil où une bille, lancée par un croupier, termine sa course sur un numéro compris entre 0 et 36 (soit 37 numéros)

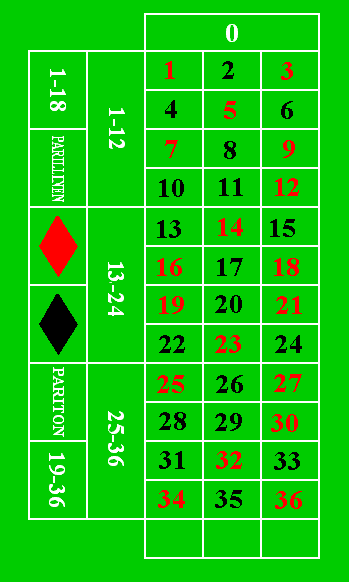
Les règles de mise sont assez complexes. Nous en retiendrons deux :

• On peut miser sur la couleur :

  • rouge ou noir

• On peut mise sur un numéro :

Votre travail : à l’ade d’un programme, simulez les chances de gain pour ces deux règles en sachant que le 0 appartient à la banque