doomsday

C1-ALGO-08 : algorithme du jugement dernier (Doomsday algorithm)#

Objectifs pédagogiques#

  1. Appliquer un algorithme décrit par un algorigramme

  2. Dessiner un algorigramme sur la base d’un algorithme écrit en français

Historique#

L’algorithme du jour du Jugement dernier, ou méthode des jours-pivots, ou méthode du clavedi, ou méthode de Conway (en anglais : Doomsday rule ou Doomsday algorithm), est une méthode de calcul du jour de la semaine correspondant à une date précise. Cet algorithme fut élaboré à l’origine par John Horton Conway (1937-2020), célèbre mathématicien britannique connu notamment pour être l’inventeur du Jeu de la vie.

Algorithme du Jour du Jugement dernier#

Il se déroule en trois étapes :

  1. Etape 1 : Déterminer la balise du siècle

  2. Etape 2 : Calculer le jour-clé de l’année

  3. Etape 3 : Choisir le jour-pivot

Pour la troisième étape, il s’agit d’avoir un sous-algorithme qui renvoie Vrai si l’année considérée est bisextile

Etape 1 : Déterminer la balise du siècle#

Le cycle des dates et des jours de semaine du calendrier grégorien se reproduit à l’identique tous les 4 siècles

Siècles

1600
2000
2400
…

1700
2100
2500
…

1800
2200
2600
…

1900
2300
2700
…

Balise du siècle

2

0

5

3

Etape 2 : Calculer le jour-clé de l’année#

  • l’année est donnée par ses deux derniers chiffres

  • le calcul se fait selon l’algorithme décrit par l’algorigramme suivant

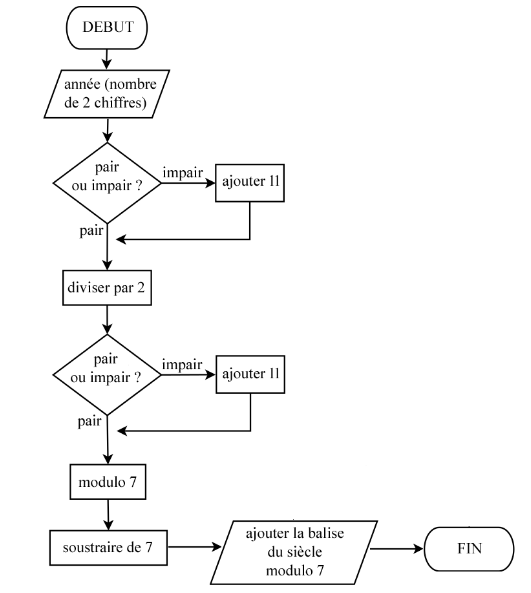
doomsday

Le chiffre obtenu à la fin de l’algorithme est un jour de semaine

Chiffre

Jour

0

Dimanche

1

Lundi

2

Mardi

3

Mercredi

4

Jeudi

5

Vendredi

6

Samedi

Etape 3 : Choisir un jour-pivot#

Avant de choisir le jour-pivot, il s’agit de déterminer si l’année considérée est ordinaire ou bisextile

Algorithme : année bisextile#

  • SI l’année est un multiple de 4 alors elle est bisextile

    • SAUF si l’année est divisible par 100 MAIS pas par 400

  • SINON elle n’est pas bisextile

bisextile

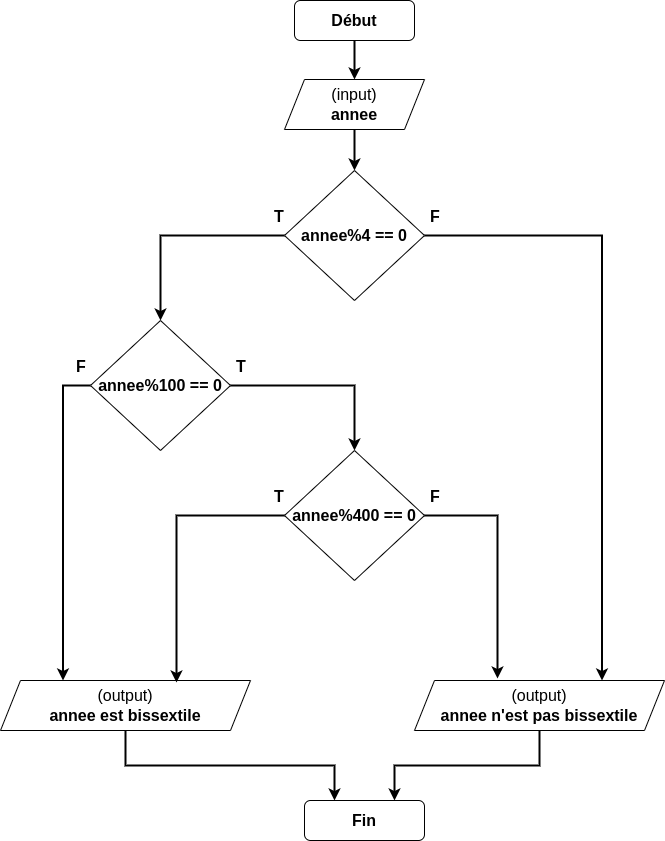
annee = 1964

if (annee%4 != 0) :
    print(str(annee)+" n'est pas une année bisextile")
else:
    if (annee%100 != 0) :
        if (annee%400 != 0) :
            print(str(annee)+" est une année bisextile")
        else:
            print(str(annee)+" n'est pas une année bisextile")
    else:
        print(str(annee)+" est une année bisextile")

1964 est une année bisextile

Une fois le jour-clé déterminé, on choisit un jour proche de celui recherché selon le tableau suivant. Il permettra de calculer facilement le jour de la semaine correspondant à la date recherchée.

Remarque Si le jour-clé est un mardi, toutes les dates du tableau pour l’année considérée sont aussi un mardi.

Janvier

Février

Mars

Avril

Mai

Juin

Juillet

Août

Septembre

Octobre

Novembre

Décembre

Ordinaire

10

28

14

4

9

6

11

8

5

10

7

12

Bisextile

11

29

14

4

9

6

11

8

5

10

7

12

Exemples#

18 janvier 1967#

  • Etape 1

    • 1900 correspond à la balise du siècle 3

  • Etape 2

    • 67 est impair, donc 67 + 11 = 78

    • 78 / 2 = 39

    • 39 est impair donc 39 + 11 = 50

    • 50 modulo 7 = 1

    • 7 - 1 = 6

    • (6+3) modulo 7 = 9 modulo 7 = 2

    • 2 le jour-clé de l’année est un mardi

  • Etape 3

    • 1967 est une année ordinaire

    • le 10 janvier (jour-pivot) est un mardi.

    • 10 + 7 = 17 est aussi un mardi. Le 18 est donc un mercredi