TP2-PROG-02 : Approche pratique de la complexité : Pile ou face

complexite

TP2-PROG-02 : Approche pratique de la complexité : Pile ou face#

Objectifs pédagogiques#

  • Découvrir la bibliothèque de fonctions random pour les nombres aléatoires

  • être capable de mesurer le temps d’un bloc d’instructions dans un code informatique

  • déduire la complexité temporelle d’un algorithme

Les nombres aléatoires#

Un nombre aléatoire est un nombre quelconque tiré au hasard entre deux bornes.

Remarque : il est mathématiquement hors du cadre d’études gymnasiales de définir exactement ce qu’est une suite de nombres aléatoires. Je vous renvoie à random.org

Ce que l’on sait, c’est qu’il est impossible pour un ordinateur de produire une suite de nombres aléatoires puisque par définition, un ordinateur suit des algorithmes.

Comment produire une suite de nombre aléatoires ?#

En utilisant deux concepts :

  1. Le fait qu’aujourd’hui, il est impossible pour une machine de prédire un phénomène physique suffisamment complexe

  2. Utiliser des mesures de ce phénomène physique. Par exemple : le bruit d’un carrefour, un film live d’un arbre au vent, la position des nuages, etc..

Générateur de nombres pseudo-aléatoires en Python#

Un ordinateur produit des nombres pseudo-aléatoires. Il existe une bibliothèque de fonctions dans Python qui nous permet de le faire. Cette bibliothèque s’appelle random. Elle contient notamment une fonction qui permet de tirer un nombre aléatoire entier entre deux bornes :

import random
borneInf = 0
borneSup = 10
aleatoire = random.randint(borneInf, borneSup)

Ce programme tirera à chaque exécution un nombre aléatoire compris entre 0 et 10

Graine de départ du générateur#

Informatiquement, le générateur de nombres aléatoires est un algorithme. Cet algorithme a besoin d’un point de départ pour pouvoir commencer à générer des nombres aléatoires. Ce point de départ est appelé graine (ou seed en anglais). Il est rare que l’on veuille préciser une graine spécifique : on prend généralement le temps (soit le nombre de secondes qui se sont écoulées depuis le 1 janvier 1970 (une date nommée ère). Mais il se peut que l’on veuille toujours réutiliser la même suite de nombres aléatoires. Dans ce cas, on en précisera la graine.

Le code suivant produira systématiquement les mêmes nombres aléatoires

import random
borneInf = 0
borneSup = 10
graine = 1000
random.seed(graine)
for i in range(10):
    aleatoire = random.randint(borneInf, borneSup)
    print(aleatoire)

6
10
1
6
5
1
7
2
8
6

Exercice 1 : Nombres aléatoires#

Voici un programme qui permet de tirer un nombre aléatoire et de l’afficher:

import random
borneInf = 2
borneSup = 10
aleatoire = random.randint(borneInf, borneSup)
print(aleatoire)

4

  • modifiez les bornes borneInf et borneSup

  • observez que votre programme donne effectivement un nombre aléatoire compris entre ces bornes

Exercice 2 : Pile ou face ?#

Lorsqu’on lance une pièce de monnaie en l’air, elle a une chance sur deux de retomber sur face, une chance sur deux sur pile.

Vérifions que la bibliothèque random nous donne bien les bonnes valeurs.

  • Ecrivez un programme qui tire un nombre aléatoire entier entre 0 (pile) et 1 (face)

Exécutez votre programme plusieurs fois. Est-ce que l’ordinateur tire bien des nombres aléatoires ?

Exercice 3 : Probabilités de pile, probabilité de face#

Modifiez votre programme de pile ou face pour qu’il tire nbrTirs fois la pièce.

  • comptez le nombre de piles et de face (en stockant la valeur intermédiaire dans deux variables nbrPile et nbrFace

  • Vérifiez que le résultat est le bon en calculant la probabilité d’un tir pile (probPile = nbrPile/nbrTirs) et la probabilité d’un tir face (probFace = nbrFace/nbrTirs)

Exercice 4 : Mesurer le nombre d’opérations#

Observez votre code et comptez le nombre d’opérations (instructions) par itération de la boucle. Modifiez ensuite votre code pour que le nombre d’opérations ou d’instructions soit comptabilisés. Stockez cette valeur dans une variable nbrOps

Mesure du temps dans un code#

Dans Python, il est possible de mesurer le nombre de secondes entre deux lignes d’un programme. Cela se fait en important la bibliothèque time et en appelant une fonction de timing (qui retourne le temps) : time.time().

import time

start = time.time()

# block de code à mesurer

end = time.time()

print("Temps passé dans le bloc de code à mesurer : ",(end-start))

Exercice 5: Mesurer le temps#

Modifiez votre code de pile ou face pour qu’il mesure le temps entre le début et la fin du code. Stockez cette valeur dans une variable t

Exercice 6 : Complexité de Pile ou Face#

Dans un tableau Excel, placez les valeurs de \(N\) (nombre de tirs), le nombre d’opérations (instructions) mesurées \(NbrOps\) et le temps (\(f(N)\)). Quelle est la classe de complexité de cet algorithme ?

La console de Thonny ne permet pas de copier-coller plus de 1000 lignes de sortie (print). Afin de pouvoir créer des graphiques dans Excel, il est nécessaire d’enregistrer les valeurs N, Nbrops et temps dans un fichier de type CSV. Voici un code permettant de créer un tel fichier, d’enregistrer des données par ligne (sous la forme d’une liste), et de refermer le fichier. Le fichier final nom_de_fichier.csv se trouvera dans le même dossier que le fichier source Python.

import csv
f = open("nom_de_fichier.csv", "w")
writer = csv.writer(f)

...
data = [n, altitude_max]
writer.writerow(data)
...

f.close()

Dans Excel, vous pouvez importer ensuite les données contenues dans le fichier CSV (Coma Separated Values) : Fichier -> Importer -> CSV puis préciser que le délimiteur est une virgule (un Coma en anglais).

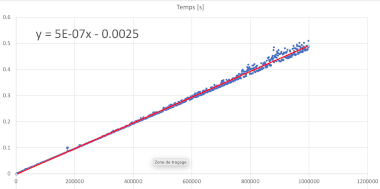
L’insertion d’un fichier vous permet au final de créer un grpahique à partir des données importées et de déduire la complexité de l’algorithme.

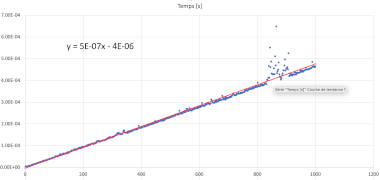
time1

ou en augmentant la taille d’entrée N (attention tout de même au temps d’exécution !!)

time1

Contents