C1-ALGO-04 : Traces algorithmiques

traces

(source : image générée par IA)

C1-ALGO-04 : Traces algorithmiques#

Objectifs pédagogiques#

  • comprendre les différentes étapes d’un algorithme avec un exemple d’entrée

  • vérifier l’évolution des variables en suivant un algorigramme ou un programme informatique

  • appliquer sur un exemple

Traces Définition#

Une trace algorithmique (on parle aussi de trace d’exécution) est un tableau qui permet de suivre l’évolution des variables et les différentes étapes de l’exécution d’un algorithme, symbole après symbole pour un algorigramme, ligne par ligne pour un programme (ou un algorithme écrit en français).

La trace permet de :

  • comprendre l’algorithme en utilisant un exemple d’entrée(s)

  • identifier d’éventuelles erreurs (bugs)

Méthodologie pour construire une trace#

La création d’une trace d’un algorithme se déroule en étapes.

1 : Identifier les variables#

Repérer et identifier toutes les variables : entrées, sorties et variables internes à l’algorithme

2 : construire le tableau#

  • la première colonne contient le numéro de chaque étape de l’algorithme

  • la seconde colonne contient l’instruction (opération, action, etc..)

  • ensuite, on ajoute une colonne par variable. Cela nous permettra de placer la valeur de chaque variable à chaque étape

N°

instruction

variable1

variable2

variable3

1

3 : Lire l’algorithme symbole par symbole (ou ligne par ligne)#

Il s’agit d’exécuter mentalement chaque instruction dans l’ordre de la même façon que l’ordinateur.

Pour chaque symbole ou ligne :

  • si c’est une affectation (signe =) : changer la valeur de la variable correspondante

  • si c’est un test/condition ou une boucle : tester la condition avec les valeurs actuelle (celles de la ligne précédente)

  • si c’est une sortie, alors afficher la valeur actuelle

  • si la valeur d’une variable est inconnue, alors on place ?

4 : Remplir le tableau#

Ajouter une ligne pour chaque symbole ou chaque instruction exécutée.

  • une instruction = une ligne

  • si une instruction est répétée (dans une boucle), alors elle représente plusieurs lignes dans la trace (autant que la boucle est répétée)

  • après chaque affectation, mettre à jour immédiatement la valeur de la variable concernée.

5. Gérer les boucles#

C’est la seule exception : il faut vérifier avant d’entrer dans la boucle si la condition de sortie est remplie. Si la condition de sortie est True, alors il ne faut pas exécuter le bloc d’instruction de la boucle, si c’est True, alors on les exécute. A chaque tour de la boucle :

  • exécuter le bloc d’instructions (une ligne par instruction)

  • mettre à jour les variables

  • re-vérifier la condition de sortie à chaque exécution du bloc d’instructions

6. Vérification de la cohérence globale#

  1. Toutes les instructions ont-elles été exécutée (l’une n’a-t-elle pas été oubliée ?)

  2. y a-t-il une seule instruction par ligne

  3. toutes les variables ont-elles été définies ?

  4. la condition de sortie des boucles sont-elles atteintes ?

  5. la sortie est-elle cohérente ?

Exemple 1 : Algorithme d’Euclide#

Construisons la trace de l’algorithme de recherche du PGDC de deux nombres entiers m et n d’Euclide.

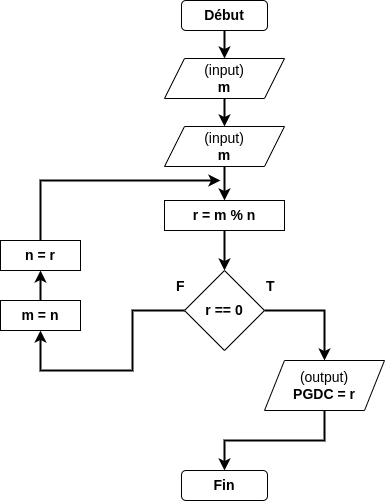
Euclide

En suivant la méthodologie :

  1. Les variables sont : m, n, r, et PGDC

  2. Le tableau à remplir est le suivant :

N°

instruction

m

n

r

PGDC

1

  1. l’algorigramme est lu en choisissant un exemple d’entrée.

  2. Remplissons le tableau avec - par exemple - les entrées : m = 30 et n = 21 :

N°

instruction

m

n

r

PGDC

1

(input) m

30

?

?

?

2

(input) n

30

21

?

?

3

r = m % n

30

21

9

?

4

condition r == 0 : False

30

21

9

?

5

m = n

21

21

9

?

6

n = r

21

9

9

?

7

r = m % n

21

9

3

?

8

condition r == 0 : False

21

9

3

?

9

m = n

9

9

3

?

10

n = r

9

3

3

?

11

r = m % n

9

3

0

?

12

condition r == 0 : True

9

3

0

?

13

(output) PGDC == n

9

3

0

3

Exercice 1 : Un algorigramme#

Etablissez la trace de l’algorithme suivant avec les entrées A = 5 et B = 4 :

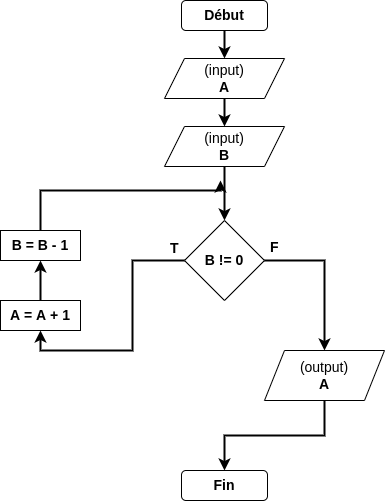
somme

Question : Que contient la variable A ?

Exercice 2 : Un code en Python#

Etablissez la trace du programme suivant avec n = 6

a = 1
b = 1
n = int(input("Combien de nombres de voulez-vous ? "))
i = 0
print(a)
print(b)
while i < n-2:
    a = a + b
    b = a - b
    print(a)
    i = i + 1

---------------------------------------------------------------------------
StdinNotImplementedError                  Traceback (most recent call last)
Cell In[1], line 3
      1 a = 1
      2 b = 1
----> 3 n = int(input("Combien de nombres de voulez-vous ? "))
      4 i = 0
      5 print(a)

File ~/.local/pipx/venvs/jupyter-book/lib/python3.11/site-packages/ipykernel/kernelbase.py:1274, in Kernel.raw_input(self, prompt)
   1272 if not self._allow_stdin:
   1273     msg = "raw_input was called, but this frontend does not support input requests."
-> 1274     raise StdinNotImplementedError(msg)
   1275 return self._input_request(
   1276     str(prompt),
   1277     self._parent_ident["shell"],
   1278     self.get_parent("shell"),
   1279     password=False,
   1280 )

StdinNotImplementedError: raw_input was called, but this frontend does not support input requests.

Question : quelle est cette suite ?

Contents