C2-ALGO-04 : Introduction à la théorie des graphes
Contents
C2-ALGO-04 : Introduction à la théorie des graphes#
Objectifs pédagogiques#
connaître les différentes utilisation des graphes dans l’informatique
connaître la définition d’un graphe
être capable de construire et lire une matrice d’adjacence
appliquer l’algorithme de Dijkstra du plus court chemin sur un graphe
Exemple introductif#
Il est d’usage d’introduire la théorie des graphes en présentant le célèbre problème dit des sept ponts de Königsberg.
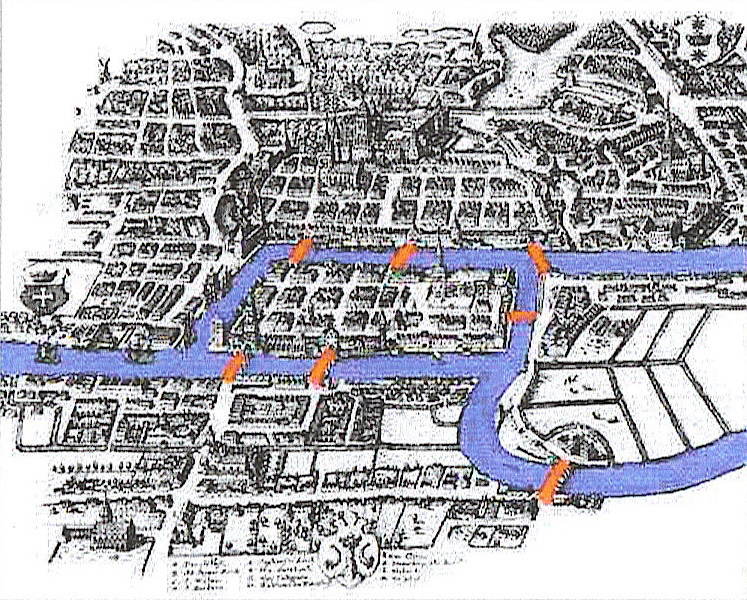
Le problème est le suivant : La ville de Königsberg (aujourd’hui Kaliningrad), du temps de Leonhard Euler le célèbre mathématicien et physicien suisse qui l’a résolu, est construite dans l’estuaire du fleuve Pregolia sur 5 îles reliées par des ponts. Ces ponts étaient au nombre de 7 du temps d’Euler. Le problème consiste à partir d’un point de départ au choix, de passer une et une seule fois sur chacun des sept ponts et à revenir au point de départ.
Solution : il n’existe pas de solution à ce problème. La démonstration (faite par Euler) dépasse largement le cadre de ce cours d’informatique
Utilisation des graphes#
Les graphes sont utilisés dans divers domaines :
Les réseaux informatiques
Les réseaux sociaux
La cartographie
Les réseaux de neurones (et donc l’IA)
Quelques exemples#
Les réseaux informatiques#
L’image ci-dessous représente le graphe des requêtes vers les sites tiers ainsi que les cookies déposés par ces derniers avec lesquels l’internaute a interagi. Il s’agit d’une extension libre du navigateur libre Firefox
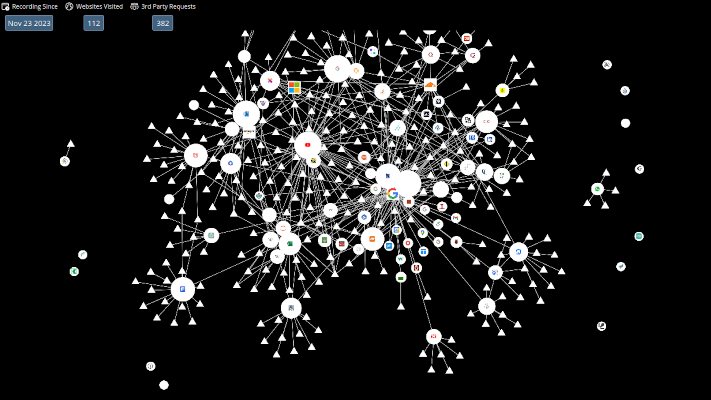
La cartographie#
L’image ci-dessous représente une solution du célèbre problème du voyageur de commerce (Travaling Salesman Problem). L’idée est de trouver le chemin le plus court qui passe une seule fois par chacun des sommets (représentant ici les capitales des états amércains)
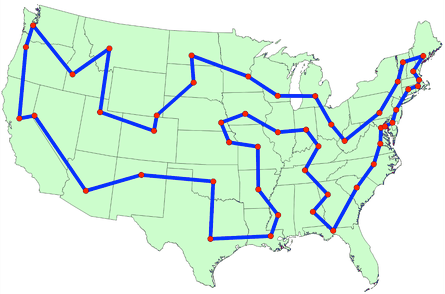
Les réseaux de neurones#
L’image ci-dessous représente un réseau de neurones artificielles, l’un des composants de base vers la créations d’une intelligence artificielle.
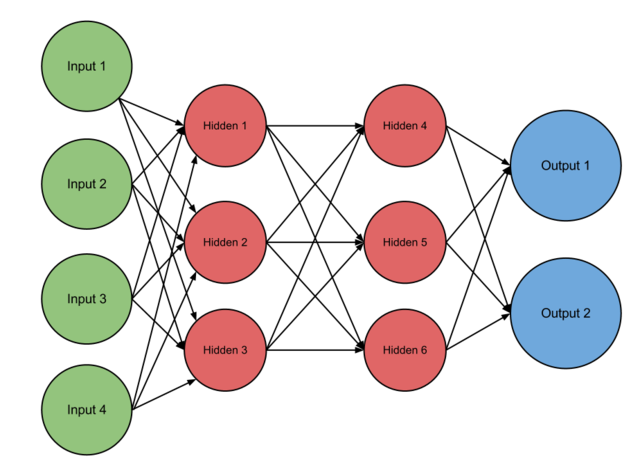
Définition : graphe#
Un graphe est une structure composée de deux objets :
Une liste de sommets. Un sommet peut avoir un nom
Une liste d’arêtes qui relient les sommets. L’arête peut possèder un poids qui représente n’importe quelle grandeur (une longueur, un coût, etc..)
La représentation courante est graphique avec des cercles pour les sommets et des lignes pour les arêtes.
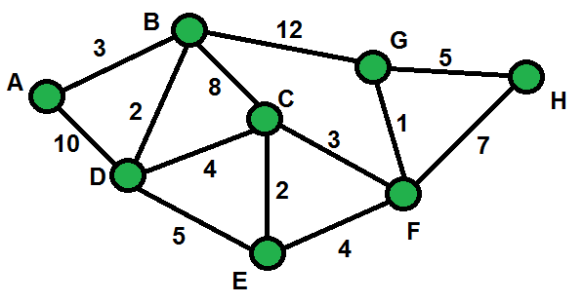
Orientation#
Un graphe est dit orienté lorsque les arêtes sont des flèches avec une direction.
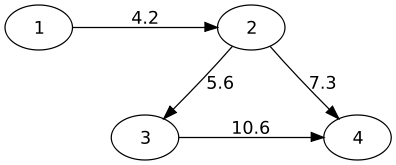
Définition : matrice d’adjacence#
Lorsque le graphe est trop complexe pour être représenté graphiquement, on utilise un tableau. En mathématique, on parle de matrice.
Une matrice d’adjacence pour un graphe à n sommets est un tableau de dimension n x n dont chaque élément qui ne se trouve pas sur la diagonale contient le poids de l’arête qui relie les deux sommets à l’intersection de la colonne et de la ligne. Si les arêtes ne possèdent pas de poids, alors on indiquera 1 si une arête existe, 0 sinon.
Exemple#
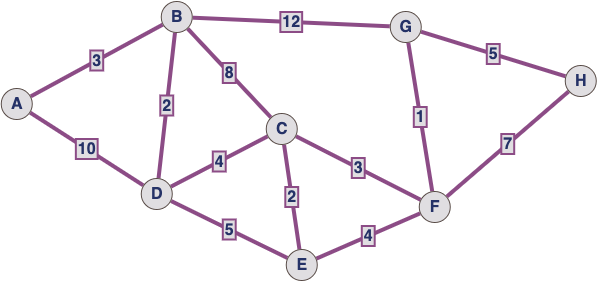
La matrice d’adjacence se présente alors ainsi :
A |
B |
C |
D |
E |
F |
G |
H |
|
|---|---|---|---|---|---|---|---|---|
A |
3 |
0 |
10 |
0 |
0 |
0 |
0 |
|
B |
3 |
8 |
0 |
0 |
0 |
12 |
0 |
|
C |
0 |
8 |
4 |
2 |
3 |
0 |
0 |
|
D |
10 |
0 |
4 |
5 |
0 |
0 |
0 |
|
E |
0 |
0 |
2 |
5 |
4 |
0 |
0 |
|
F |
0 |
0 |
3 |
0 |
4 |
1 |
7 |
|
G |
0 |
12 |
0 |
0 |
0 |
1 |
5 |
|
H |
0 |
0 |
0 |
0 |
0 |
7 |
5 |
Mathématiquement on la présente ainsi :
Exercice 1 : matrice d’adjacence#
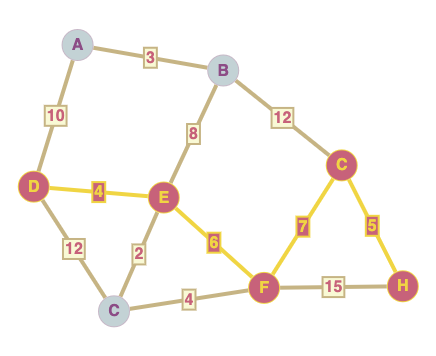
Ecrivez la matrice d’adjacence du graphe suivant :
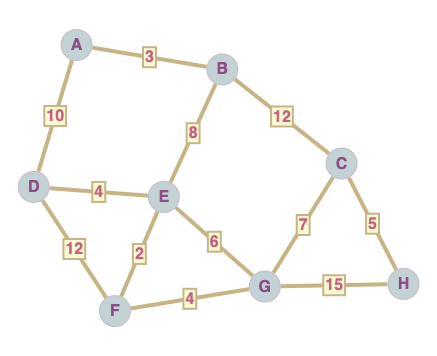
Exercice 2 : chemin le plus court 1#
Quel est le chemin le plus court entre les sommets D et H ?
Exercice 3 : chemin le plus cours 2 !#
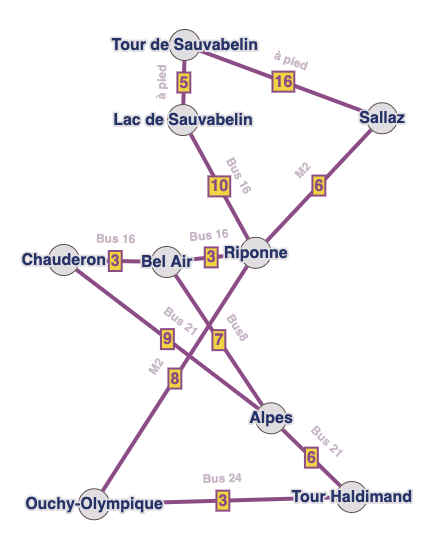
Pour le trajet Tour Haldimand -> Tour de Sauvabelin, Google Maps propose
Bus 24 jusqu’à Ouchy (3’), M2 jusqu’à Sallaz (14’), puis à pied (16’)
Bus 21 jusqu’à Alpes (6’), bus 8 jusqu’à Bel Air (7’), bus 16 jusqu’à Sauvabelin (13’), puis à pied (5’)
Bus 21 jusqu’à Chauderon (18’), bus 16 jusqu’à Sauvabelin(16’), puis à pied (5’)
1h15 à pied, ça fait du bien !
Quel trajet mettrait le moins de temps ?
Faisons le graphe !
Algorithme de Dijkstra#
L’algorithme de Dijkstra consiste à partir d’un point (par exemple A) à trouver le chemin le plus court jusqu’à couvrir l’ensemble du graphe.
On ne prend pas deux fois un chemin car on construit un arbre couvrant.
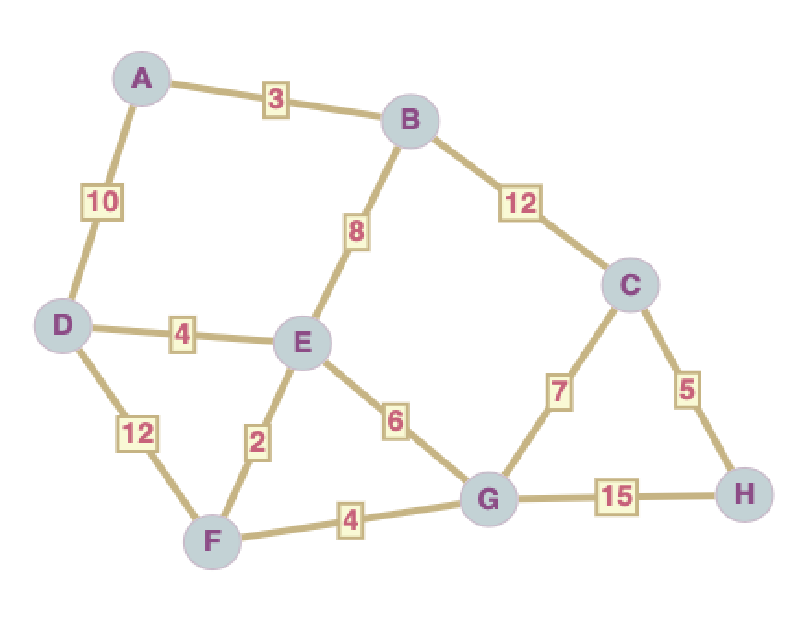
Dans cet exemple, il y a deux chemins qui partent de A et finissent à G de longueur 17 : A-B-E-F-G et A-B-E-G
Exercice 4 : Dijkstra#
Construire l’arbre recouvrant dans le graphe suivant :
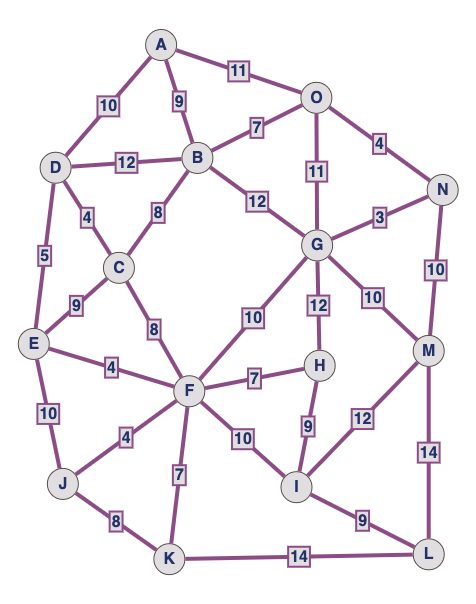
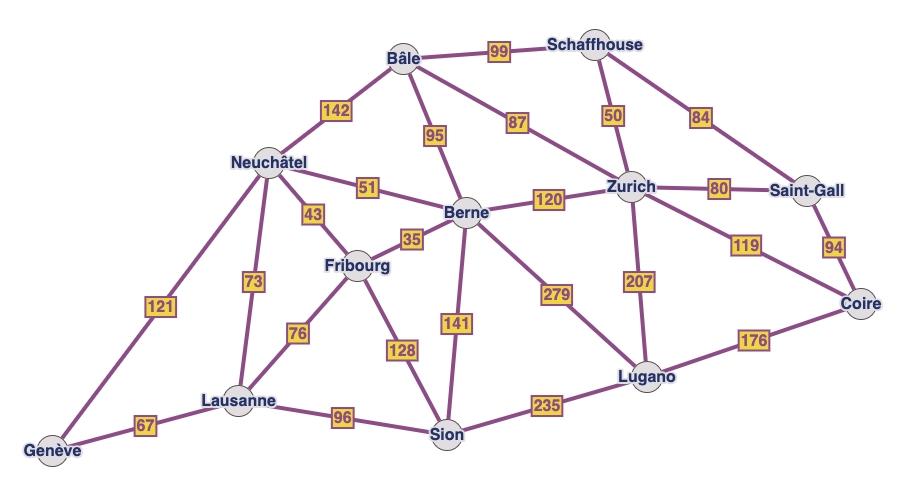
Exercice 5 : Villes suisses#
Sur ce graphe, on indique les distances entre quelques villes importantes en Suisse.
Quel est le chemin le plus court entre Genève et Coire ?
Solution#
Voici la matrice d’adjacence entre les villes
Lausanne |
Genève |
Neuchâtel |
Fribourg |
Berne |
Zürich |
Lugano |
Sion |
Bâle |
Schaffhouse |
St-Gall |
Coire |
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|
Lausanne |
0 |
67 |
73 |
76 |
111 |
231 |
331 |
96 |
206 |
281 |
311 |
350 |
Genève |
67 |
0 |
121 |
143 |
172 |
292 |
398 |
163 |
263 |
342 |
372 |
411 |
Neuchâtel |
73 |
121 |
0 |
43 |
51 |
171 |
330 |
169 |
142 |
221 |
251 |
290 |
Fribourg |
76 |
143 |
43 |
0 |
35 |
155 |
314 |
128 |
130 |
205 |
235 |
274 |
Berne |
111 |
172 |
51 |
35 |
0 |
120 |
279 |
141 |
95 |
170 |
200 |
239 |
Zürich |
231 |
292 |
171 |
155 |
120 |
0 |
207 |
261 |
87 |
50 |
80 |
119 |
Lugano |
331 |
398 |
330 |
314 |
279 |
207 |
0 |
235 |
294 |
257 |
270 |
176 |
Sion |
96 |
163 |
169 |
128 |
141 |
261 |
235 |
0 |
246 |
311 |
341 |
380 |
Bâle |
206 |
263 |
142 |
130 |
95 |
87 |
294 |
236 |
0 |
99 |
167 |
206 |
Schaffhouse |
281 |
342 |
221 |
205 |
170 |
50 |
257 |
311 |
99 |
0 |
84 |
169 |
St-Gall |
311 |
372 |
251 |
235 |
200 |
80 |
270 |
341 |
167 |
84 |
0 |
94 |
Coire |
350 |
411 |
290 |
274 |
239 |
119 |
176 |
380 |
206 |
169 |
94 |
0 |
Solution des exercices#
Exercice 1#
La matrice d’ajacence est la suivante :
A |
B |
C |
D |
E |
F |
G |
H |
|
|---|---|---|---|---|---|---|---|---|
A |
0 |
3 |
0 |
10 |
0 |
0 |
0 |
0 |
B |
3 |
0 |
12 |
0 |
8 |
0 |
0 |
0 |
C |
0 |
12 |
0 |
0 |
0 |
0 |
7 |
5 |
D |
10 |
0 |
0 |
0 |
4 |
12 |
0 |
0 |
E |
0 |
8 |
0 |
4 |
0 |
2 |
6 |
0 |
F |
0 |
0 |
0 |
12 |
2 |
0 |
4 |
0 |
G |
0 |
0 |
7 |
0 |
6 |
4 |
0 |
15 |
H |
0 |
0 |
5 |
0 |
0 |
0 |
15 |
0 |
Exerice 2#
Voici une solution :
Code Python Dijkstra#
Le code suivant permet de calculer la longueur des chemins en utilisant la matrice d’adjacence et l’algorithme de Dijkstra
# Code permettant de calculer l'algorithme de Dijkstra
# sur le graphe du cours C2_ALGO_04
import random
INF = 100000
nbr = 8
A = [ 0, 3, 0,10, 0, 0, 0, 0]
B = [ 3, 0,12, 0, 8, 0, 0, 0]
C = [ 0,12, 0, 0, 0, 0, 7, 5]
D = [10, 0, 0, 0, 4,12, 0, 0]
E = [ 0, 8, 0, 4, 0, 2, 6, 0]
F = [ 0, 0, 0,12, 2, 0, 4, 0]
G = [ 0, 0, 7, 0, 6, 4, 0,15]
H = [ 0, 0, 5, 0, 0, 0,15, 0]
graph = [A,B,C,D,E,F,G,H]
# Nomme le sommet à partir duquel on calcule l'arbre couvrant
premier = 3
noeuds = ["A","B","C","D","E","F","G","H"]
nbr = len(graph)
visites = [False] * nbr
distances = [INF] * nbr
distances[premier] = 0
for i in range(nbr):
# Recherche des noeuds avec la distance minimum
min_distance = INF
min_index = -1
for v in range(nbr):
if not visites[v] and distances[v] < min_distance:
min_distance = distances[v]
min_index = v
visites[min_index] = True
# Recalcul des distances depuis le noeud
for v in range(nbr):
if graph[min_index][v] > 0 and not visites[v]:
new_distance = distances[min_index] + graph[min_index][v]
if new_distance < distances[v]:
distances[v] = new_distance
print("Distance depuis la source : ",noeuds[premier])
print("Noeud","\t","Distance")
for i in range(nbr):
print(noeuds[i],"\t",distances[i])
Distance depuis la source : D
Noeud Distance
A 10
B 12
C 17
D 0
E 4
F 6
G 10
H 22
