exercer

C2-ALGO-03 : Complexité des algorithmes (suite)#

Objectifs pédagogiques#

  • déduire la complexité temporelle de quelques algorithmes classiques

Méthode#

  • On calcule toujours la complexité dans le pire des cas

  • la complexité d’un algorithme est indépendante d’une implémentation quelconque et d’une machine quelconque

  • On utilise la notation de Landau Big O ( \(f(n) = \mathcal O (g(n))\). On s’intéresse au comportement asymptotique de la complexité. Soit le terme dominant

    • Exemple : si le temps varie comme \(f(n) = n^3 + 6n -3 = 0\) alors le comportement asymptotique de l’algorithme est \(\mathcal O (n^3)\)

  • Chaque opération ou instruction vaut \(1\) unité de temps :

    • affectation d’une variable

    • une entrée

    • une sortie

    • une comparaison (un test)

    • etc..

  • Chaque boucle rajoute le nombre d’unité de temps correspondant à toutes les unités de temps consommées dans le corps de la boucle entre chaque bornes.

  • Chaque fonction rajoute le nombre d’unité de temps correspondant à toutes les unités de temps consommées dans la fonction

  • On fait varier la taille des entrées et on estime le nombre d’unités de temps.

Exercice 1 : Comportement asymptotique \(\mathcal O\)#

Pour chaque fonction suivante, donnez la classe de complexité correspondante :

  • \(f(n) = 3n^2 + 2n + 56\)

  • \(f(n) = 4n + \sqrt{n} + 3\)

  • \(f(n) = 2n^4 + 3n^2 + log_2(n)\)

  • \(f(n) = n^{100} + 2^n + 4\)

  • \(f(n) = 3n~log_2(n) + 34\)

  • \(f(n) = n + 2n~log_2(n)\)

  • \(f(n) = 193000 + n!\)

Exercice 2 : Quelques algorithmes.#

Pour chacun des codes ou algorigrammes suivants :

  1. Décrivez en français ce que fait l’algorithme

  2. En suivant la méthode décrite plus haut, trouvez la classe de complexité algorithmique

2.1 : Crible#

limite = 100
tableau = []
for i in range(limite):
    tableau.append(True)
premiers = []
for i in range(2,limite,1):
    if tableau[i] == True :
        for j in range(i*i,limite,i):
            tableau[j] = False
for i in range(limite):
    if tableau[i] == True:
        premiers.append(i)
print(premiers)

[0, 1, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97]

eratocomplexe

2.2 Un algorithme de tri#

import random
nombres = []
longueur = 10
for i in range(longueur):
    aleat = random.randint(0,longueur)
    nombres.append(aleat)
print(nombres)
for i in range(longueur,0,-1):
    for j in range(0,i-1,1):
        if nombres[j+1] < nombres[j]:
            tmp = nombres[j+1]
            nombres[j+1] = nombres[j]
            nombres[j] = tmp
print(nombres)

[5, 3, 2, 0, 5, 4, 6, 5, 9, 5]
[0, 2, 3, 4, 5, 5, 5, 5, 6, 9]

bubblecompl

2.3 Heron d’Alexandrie et ses racines#

Heron

# Racine d'Heron d'Alexandrie monitoré
# La racine à rechercher est fixée : 2.0
# Vincent Keller, 2023
import time
a = 2.0
limite = 1000000

for i in range(1000000,limite,50000):
    start = time.time()
    lim = i
    xn = a
    for i in range(lim):
        xnp1 = 0.5 * (xn + a/xn)
        xn = xnp1
    end = time.time()
    print(i,"\t",(end-start))

racine

Correction des exercices#

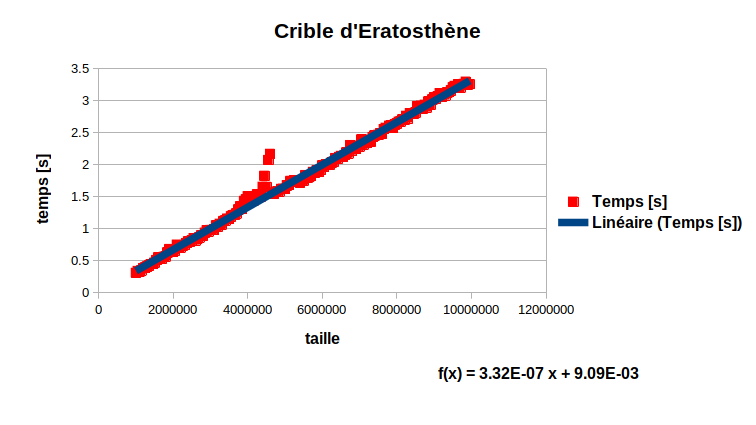
2.1 : le crible#

Description de l’algorithme en français#

Cet algorithme calcule les nombres premiers entre 1 et limite en supprimant tous les multiples d’un nombre premier trouvé. Ce nombre premier trouvé est l’index d’un tableau de booléens. Finalement, tous les nombres premiers sont placés dans une liste nommée premiers. Cet algorithme est appelé crible d’Eratosthène.

Classe de complexité algorithmique#

On observe que la grandeur qui varie est la limite supérieure dénommée limite. On observe aussi que l’on a effectivement deux boucles imbriquées ce qui exmplique un comportement asymptotique quadratique \(\mathcal O (N^2)\) . La boucle interne (celle sur l’itérateur j) est de moins en moins significative à mesure que la boucle externe (celle sur l’itérateur i).

Pour aller plus loin (facultatif) : nombre de nombres premiers entre 0 et limite

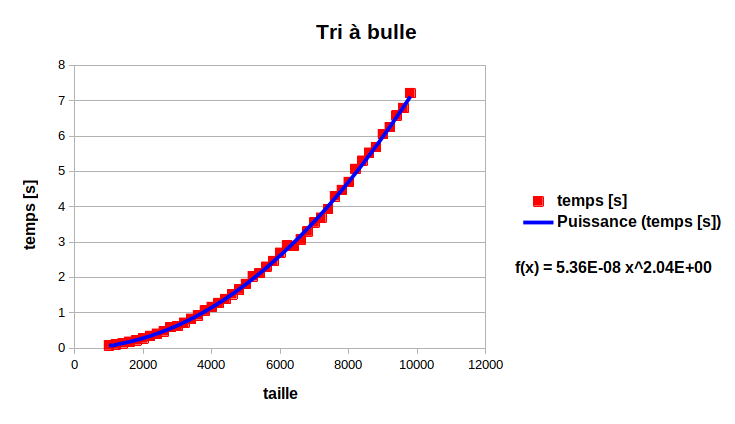
2.2 : L’algorithme de tri#

Description de l’algorithme en français#

Cet algorithme trie les éléments d’une liste de nombres aléatoires en utilisant le tri à bulles : lorsqu’un nombre se retrouve être plus grand que celui qui le devance, alors on l’inverse et on passe au suivant.

Classe de complexité algorithmique#

On observe que la grandeur qui varie est la longueur de la liste dénommée longueur. On observe que l’on a deux boucles imbriquées : l’une sur l’itérateur i et l’autre sur l’itérateur j qui encadrent un test conditionnel (si il faut inverser deux nombres ou pas). Dans le pire des cas (c’est-à-dire que la liste est triée “à l’envers”), alors la classe de complexité algorithmique est quadratique : \(\mathcal O (N^2)\)

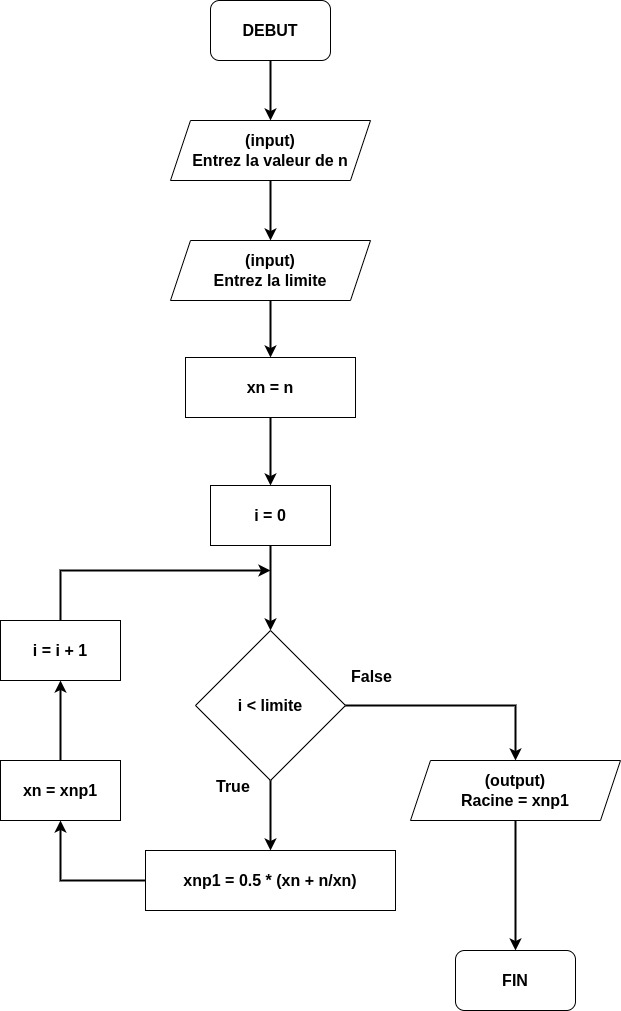
2.3 : Héron d’Alexandrie et ses racines#

Description de l’algorithme en français#

Cet algorithme calcule la racine d’un nombre n. Pour le faire, il demande une limite (borne supérieure d’une boucle) et va appliquer une formule mathématique décrite par l’algorigramme :

    xnp1 = 0.5 * (xn + n/xn)
    xn = xnp1

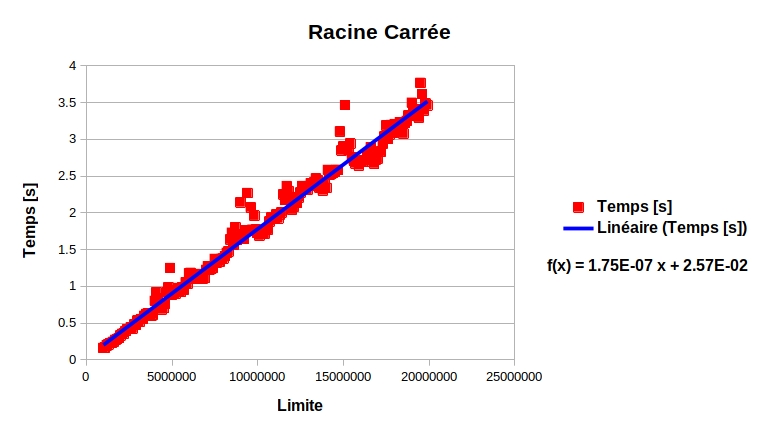
Classe de complexité algorithmique#

On observe que la grandeur qui varie est la limite supérieure de la boucle limite. Il n’y a pas d’autre boucle imbriqueé. La classe de complexité est donc linéaire : \(\mathcal O (N)\)