
TP2-PROG-05 : Conjecture de Collatz#
Programmer la suite de Syracuse en Python.
avec un programme standard
(si temps) avec un programme récursif
Algorithme de la suite de Syracuse#
ENTREE : n
SI n est PAIR, alors n = n / 2
SINON n = 3 * n + 1
La suite se termine lorsqu’on a atteint n == 1 et boucle sur la suite (1,4,2,1,4,2,…)
Définition : Conjecture#
En mathématique, une conjecture est une assertion dont on ne connaît pas encore de démonstration mathématique
Conjecture de Collatz#
La conjecture de Collatz (Lothar Collatz, né le 6.07.1910 en Allemagne et mort le 26.09.1990 en Bulgarie. Conjecture énoncée en 1937) est l’une des conjectures les plus célèbres puisqu’en dépit de sa simplicité, elle défie les mathématiciens depuis de très nombreuses années. Elle dit que la suite de Syracuse (ou problème 3x + 1), lorsqu’elle atteint 1 se répète indéfiniment sur la suite 4,2,1,4,2,1,...
Exercice 1 : Suite de Syracuse pour un n#
Programmez la suite de Syracuse en Python 3 . Ce programme prend en entrée n et affiche la suite de Syracuse jusqu’à atteindre 4.
Exercice 2 : Suite de Syracuse pour un range#
Ecrivez un nouveau programme qui affiche la suite de Syracuse pour les entiers de 5 à 1000.
Exercice 3 : Le vol#
Définition : le vol#
On appelle vol le nombre d’étapes de la suite de Syracuse avant d’arriver sur la valeur 4. Ainsi : pour n = 10, la suite de Syracuse vaut : 10, 5, 16, 8, 4, 2, 1, 4, 2, 1, .... La longueur du vol pour n = 10 vaut 4.
Calcul du vol#
Pour tout entier n entre 5 et 1000, Ecrivez un programme qui calcule son vol.
Résultat sous forme de graphique Excel#
Il est possible de copier des valeurs produites par Thonny et de les injecter dans un tableur Excel. Pour cela, il faut que les valeurs soient formatées en CSV (Comma-Separeted Values ou valeurs séparées par des virgules). Pour ce faire, il faut formatter les valeurs en utilisant l’artefact suivant :
print(n,"\t",vol)
Ce qui produira une suite de valeurs injectables dans Excel et desquelles il sera possible de créer un graphique
Exercice 4 : l’altitude maximale#
Définition : Altitude maximale#
On appelle altitude maximale pour un vol donné la valeur la plus élevèe que prendra la suite de Syracuse avant d’arriver sur 4 Par exemple pour n = 10, l’altitude maximale vaut 16
Calcul de l’altitude#
Pour tout entier n entre 5 et 1000, Ecrivez un programme qui calcule son vol.
Résultat sous forme de graphique Excel#
En suivant les mêmes consignes qu’à l’exercice 4, injectez les valeurs dans une feuille Excel et produisez un graphique. Qu’observez-vous ?
Exercice 5 (pour aller plus loin que 1000)#
Thonny n’affiche que 1000 lignes dans la console (donc les 1000 premiers résultats). C’est un problème pour créer des graphiques de vol ou d’altitude maximum entre 5 et 1000000 (par exemple).
Vol :
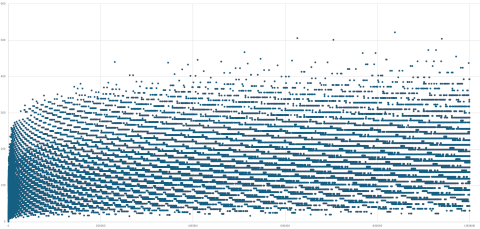
Altitude :
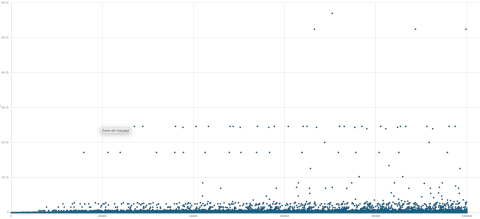
La solution (qui est utilisée dans toutes les applications professionnelles) passe par l’écriture, depuis l’application, des données dans un fichier. On importe ensuite ce fichier depuis Excel.
On utilise toujours le format CSV en important un module permettant de créer, écrire, lire ou sauvegarder dans un fichier csv:
# importation du module csv
import csv
# ouverture d'un fichier en mode écriture ("w" = write)
f = open("fichier_vol.csv", "w")
# création d'un objet d'écriture qui permettra d'écrire chaque ligne du fichier csv
writer = csv.writer(f)
...
# écriture d'une ligne (row). La ligne doit être mise sous le format d'une liste (ici data)
data = [n, altitude_max]
writer.writerow(data)
...
# en toute fin de programme, il faut fermer le fichier avec
f.close()
Modifiez votre programme pour qu’il enregistre un fichier des vol et des altitudes maximum et importez le depuis Excel
Exercice 6 (pour aller plus loin avec des fonctions)#
Reprenez votre code de l’exercice 1. Transformez le coeur de l’algorithme en une fonction. Cette fonction aura un argument (
n) et aucun retour.Réécrivez le code de l’exercice 2 en utilisant votre nouvelle fonction
Exercice 7 (pour aller vraiment très loin et résoudre la conjecture)#
Pour démontrer la conjecture de Collatz, il suffit de démontrer qu’il existe un seul n qui ne se termine pas sur la suite ...4,2,1. Ce faisant, vous gagnez beaucoup de gloire (et probablement d’argent).
Ecrivez une nouvelle fonction qui renvoie la valeur True si n se termine par 4,2,1 et False sinon. Vous pouvez ensuite modifier votre programme de l’exercice 5 et le faire tourner jusqu’à ce qu’il vous donne ce ncherché (s’il existe).
