
R1-REDO-01 Révision#
Objectifs pédagogiques#
Réviser les objets d’apprentissages sur la représentation de l’information en vue du test
représentation des nombres entiers
représentation des caractères
représentation des images
représentation du son
Représentations des nombres entiers#
Notation binaire#
Le binaire (base 2) s’écrit avec deux symboles : \([0,1]\).
Notation décimale#
En décimal (base 10), on utilise 10 symboles : \([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]\)
Notation hexadécimale#
En hexadécimal (base 16), on utilise 16 symboles : \([0,1,2,3,4,5,6,7,8,A,B,C,D,E,F]\)
Convention d’écriture#
Pour distinguer la base d’un nombre (puisque les bases se partagent des symboles), on utilise la notation par indice :
\(100_2\) est le nombre \(100\) en base \(2\)
\(300_{10}\) est le nombre \(300\) en base \(10\)
\(F8_{16}\) est le nombre \(F8\) en base \(16\)
Conversion binaire vers décimal#
on additionne les puissances de 2 en fonction de leur position:
position |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
|---|---|---|---|---|---|---|---|---|
puissance |
\(2^7\) |
\(2^6\) |
\(2^5\) |
\(2^4\) |
\(2^3\) |
\(2^2\) |
\(2^1\) |
\(2^0\) |
binaire |
\(10000000_{2}\) |
\(1000000_{2}\) |
\(100000_{2}\) |
\(10000_{2}\) |
\(1000_{2}\) |
\(100_{2}\) |
\(10_{2}\) |
\(1_{2}\) |
décimal |
\(128_{10}\) |
\(64_{10}\) |
\(32_{10}\) |
\(16_{10}\) |
\(8_{10}\) |
\(4_{10}\) |
\(2_{10}\) |
\(1_{10}\) |
Conversion de décimal vers binaire#
On soustrait la plus grande puissance de 2 contenue dans le nombre en décimal et on place un \(1\) dans la puissance correspondante.
Exemple
\(59_{10} - 1 \times 2^5 = 59_{10} - 32_{10} = 27_{10}\) donc 1
\(27_{10} - 1 \times 2^4 =27_{10} - 16_{10} = 11_{10}\) donc 1
\(11_{10} - 1 \times 2^3 = 11_{10} - 8_{10} = 3_{10}\) donc 1
\(3_{10} - 0 \times 2^2 = 3_{10}\) donc 0
\(3_{10} - 1 \times 2^1 = 3_{10} - 2_{10} = 1_{10}\) donc 1
\(1_{10} - 1 \times 2^0 = 1_{10} - 1_{10} = 0_{10}\) donc 1
Le nombre 58 s’écrit donc en binaire en lisant de haut en bas : 111011
Conversion de binaire en hexadécimal#
Il suffit de construire la table de correspondance entre la base 2 et la base 16 et de convertir le binaire par blocs de 4 bits en commençant à droite. Si le nombre de bits n’est pas divisible par 4, alors on ajoute des 0 à gauche jusqu’à obtenir un nombre de bits divisibles par 4.
Valeur binaire |
valeur héxadécimale |
|---|---|
\(0000_{2}\) |
\(0_{16}\) |
\(0001_{2}\) |
\(1_{16}\) |
\(0010_{2}\) |
\(2_{16}\) |
\(0011_{2}\) |
\(3_{16}\) |
\(0100_{2}\) |
\(4_{16}\) |
\(0101_{2}\) |
\(5_{16}\) |
\(0110_{2}\) |
\(6_{16}\) |
\(0111_{2}\) |
\(7_{16}\) |
\(1000_{2}\) |
\(8_{16}\) |
\(1001_{2}\) |
\(9_{16}\) |
\(1010_{2}\) |
\(A_{16}\) |
\(1011_{2}\) |
\(B_{16}\) |
\(1100_{2}\) |
\(C_{16}\) |
\(1101_{2}\) |
\(D_{16}\) |
\(1110_{2}\) |
\(E_{16}\) |
\(1111_{2}\) |
\(F_{16}\) |
Exemples
\(10101000_2\) (\([1010,1000]_2\)) s’écrit \(A8_{16}\)
\(0111011111_2\) (en blocs de 4 : \([01,1101,1111]_2\)) n’a pas un nombre de bits divisibles par 4, on ajoute 2 zéros à gauche : \(000111011111_2\) (en blocs de 4 : \([0001,1101,1111]_2\)) s’écrit \(1DF_{16}\)
Conversion héxadécimal en binaire#
Il s’agit de faire l’opération inverse en utilisant la même table. On supprime les zéros qui se trouvent à gauche
Exemples
\(BC_{16}\) s’écrit \(10111100_{2}\)
\(3B_{16}\) s’écrit \(00111011_{2}\) donc \(111011_{2}\)
Exercice 1#
Complétez le tableau suivant
Valeur binaire |
Valeur décimale |
valeur héxadécimale |
|---|---|---|
\(00110110_{2}\) |
||
\(1975_{10}\) |
||
\(F43B_{16}\) |
||
\(1000_{10}\) |
Représentation des caractères#
Le codage ASCII#
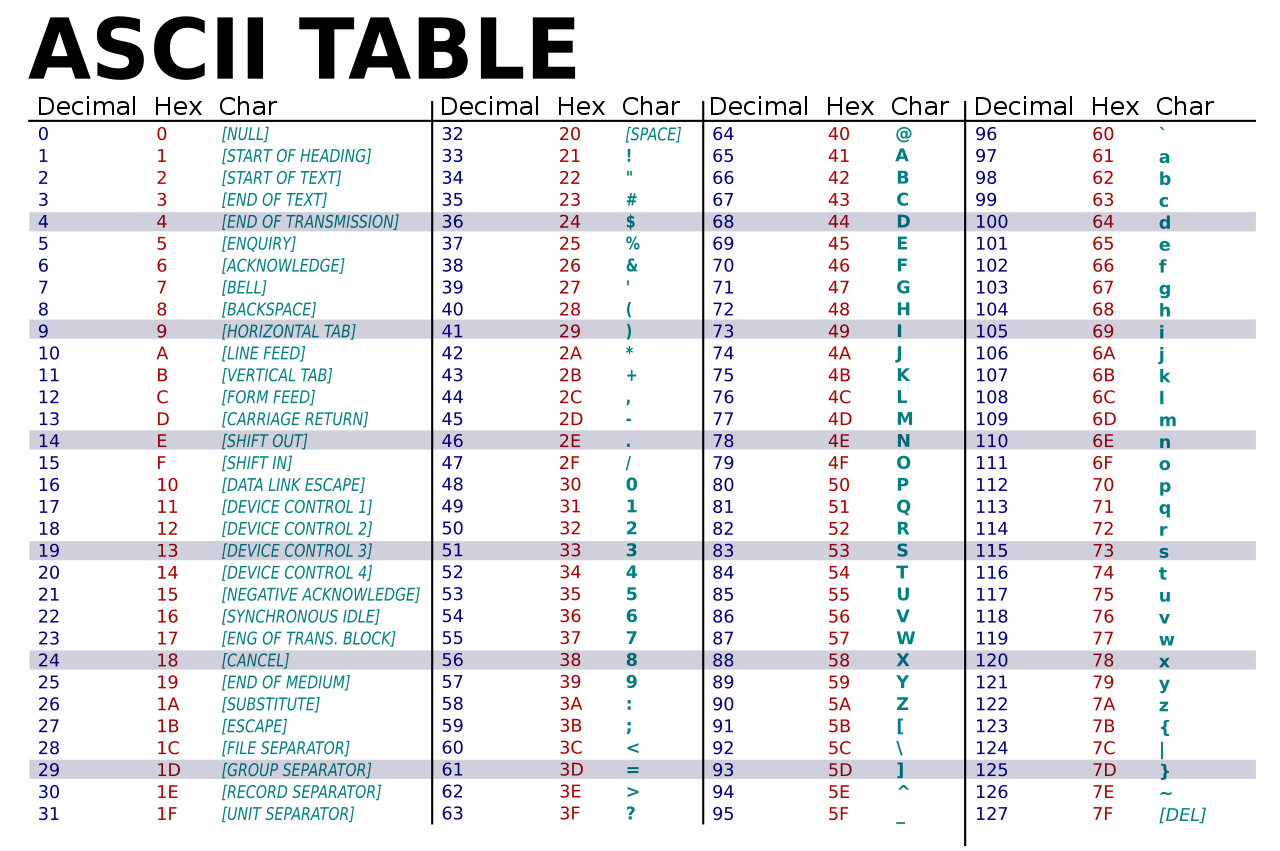
Dans ce cours nous nous limitons au codage ASCII pour les caractères. Le codage ASCII permet de coder 127 caractères différents. Il faut donc 7 bits pour coder l’entier des caractères.
La table de conversion décimal (colonne violette) - hexadécimal (colonne rouge) - caractère (colonne turquoise) se décline ainsi :
Exercice 2#
Quelle est la valeur en ASCII de la suite \(71_{10}, 121_{10}, 109_{10}, 110_{10}, 97_{10}, 115_{10}, 101_{10}\) ?
Quelle est la valeur en ASCII de la suite \(1000010_2, 1100101_2, 1100001_2, 1110101_2, 1101100_2, 1101001_2, 1100101_2, 1110101_2\) ?
Quelle est la valeur en ASCII de la suite \(62_{16}, 69_{16}, 6E_{16}, 61_{16}, 69_{16}, 72_{16}, 65_{16}\) ?
Les images matricielles#
Une image matricielle est définie par un tableau de pixels (éléments d’image). Les formats PGM/PPM décrit ce tableau en commençant en haut à gauche de l’image et termine en bas à droite, ligne par ligne.

Chaque pixel est codé avec le codage RGB (Red-Green-Blue) qui permet de coder \((2^8)^3\) couleurs différentes : du blanc \(000000_{16}\) au noir \(FFFFFF_{16}\).

Valeur du ROUGE |
Valeur du VERT |
Valeur du BLEU |
Résultat |
|---|---|---|---|
|
|
|
rouge |
|
|
|
vert |
|
|
|
bleu |
|
|
|
jaune |
|
|
|
noir |
|
|
|
blanc |
|
|
|
gris intermédiaire |
La valeur décimale (par exemple \(255\)) peut se convertir en hexadécimal avec ce qui a été vu plus haut
Exercice 3#
Quel est le nombre maximum de niveaux de gris peut-on coder avec le système RGB ?
Sans utiliser de logiciel externe, quelle est la couleur composante dominante de la couleur \((100_{10},240_{10},10_{10})\) ?
Quelle est la valeur en décimal de la couleur \((8F_{16}, 0F_{16}, 22_{16})\) et quelle est la couleur composante dominante ?
Quelle est la valeur en décimal de la couleur \((10001111_2, 00001111_2, 00100010_2)\)
Le son#
Numériser un son se déroule en 3 étapes :
Echantillonnage
Quantification
Encodage
Exercice 4#
Quelle est la plage de fréquences par l’oreille humaine ?
Si la fréquence maximum audible est de \(20\) KHz, quelle est la fréquence d’échantillonnage idéale ?
Que se passe-t-il si la fréquence d’échantillonnage est trop basse, quelles sont les fréquences qui ne sont pas codées ?
Généralités#
Afin qu’un système d’exploitation reconnaisse une suite de bits, qu’il puisse discriminer entre un caractère, un entier, une image ou un son, il faut ajouter au fichier un en-tête et qui contient des méta-données sur le format du fichier.
Réponses aux Exercices#
Exercice 1#
Valeur binaire |
Valeur décimale |
valeur héxadécimale |
|---|---|---|
\(00110110_{2}\) |
\(54_{10}\) |
\(36_{10}\) |
\(11110110111_{2}\) |
\(1975_{10}\) |
\(7B7_{10}\) |
\(1111010000111011_{2}\) |
\(62523_{10}\) |
\(F43B_{16}\) |
\(1111101000_{2}\) |
\(1000_{10}\) |
\(3E8_{16}\) |
Exercice 2#
G y m n a s e
B e a u l i e u
b i n a i r e
Exercice 3#
256
Verte
(143, 15, 34) et la dominante est rouge
(143, 15, 34)
Exercice 4#
20 Hz - 20 KHz
40 KHz ou plus (attention au sur-échantillonnage
Si la fréquence d’échantillonnage est trop faible, les fréquences hautes ne seront pas codées et seules les fréquences basses seront présentes
