C1-ALGO-03 : Les jeux de Nim#
Objectifs#
trouver la seule solution pour gagner à un jeu de stratégie pure, à deux joueurs et à somme nulle
construire l’algorigramme correspondant
Jeu de Nim#
Le jeu de Nim est un jeu de stratégie pure qui se joue à deux joueurs. Il y a toujours un gagnant et un perdant et le match nul est impossible.
Règles du jeu de Nim#
un certain nombre d’allumettes sont placées entre les deux joueurs. C’est le tas.
à chaque tour, un joueur peut retirer 1, 2 ou 3 allumettes du tas.
Fin du jeu#
Deux possibilités :
Le joueur qui prend la dernière allumette perd
Le joueur qui prend la dernière allumette gagne
Exercice 1#

Dans cet exemple, 16 allumettes ont été placées entre les deux joueurs
Consignes :#
Trouvez et expliquez, sous forme d’algorigramme, votre stratégie gagnante (si possible) pour ces 4 variantes :
l’autre joueur commence et le joueur qui prend la dernière allumette gagne
vous commencez et le joueur qui prend la dernière allumette gagne
vous commencez et le joueur qui prend la dernière alleumete perd
l’autre joueur commence et le joueur qui prend la dernière allumette perd
Exercice 2 : Variante#
Une variante au jeu de Nim existe : celle dite du “Jeu de Marienbad”.
On dispose les 16 allumettes sur 4 rangées comme le dessin ci-dessous. A chaque tour, un joueur peut prendre autant d’allumettes qu’il désire mais toutes sur la même rangée.
Celui qui prend la dernière allumette a perdu

Consignes#
Vous commencez
Trouvez la stratégie gagnante
Correction exercice 1#
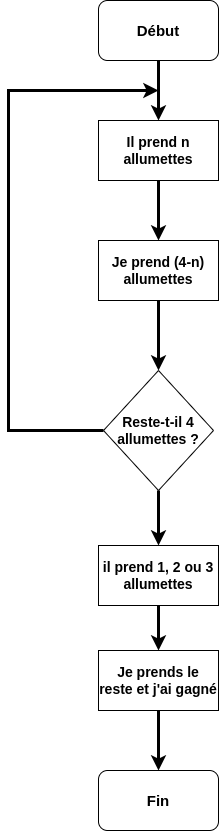
L’algorigramme pour le jeu de Nim est le suivant :
La version complète est la suivante (avec la possibilité de commencer ou de laisser l’adverssaire commencer)
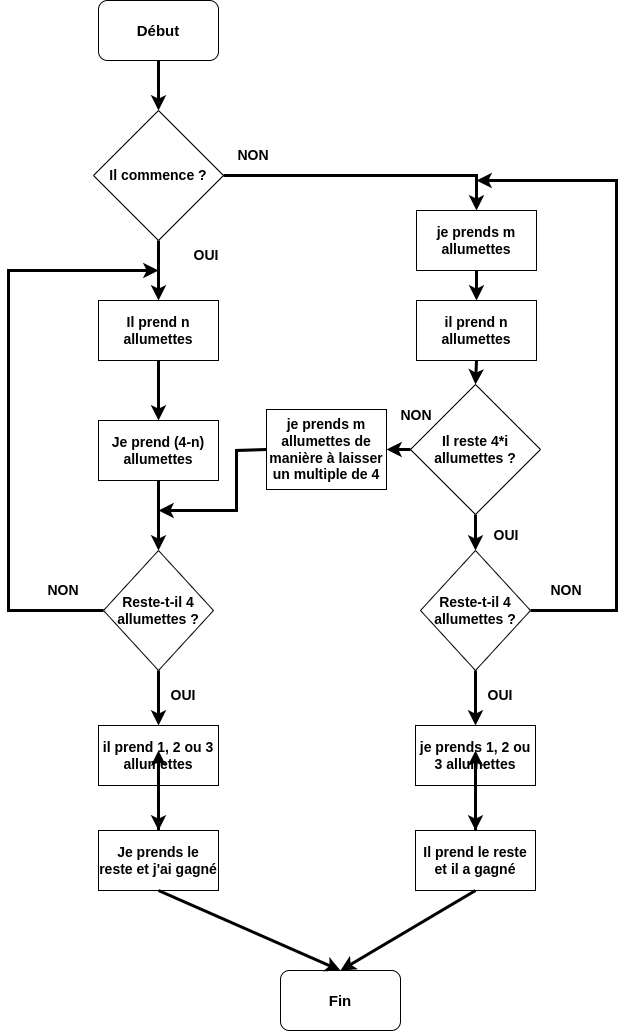
Correction exercice 2#
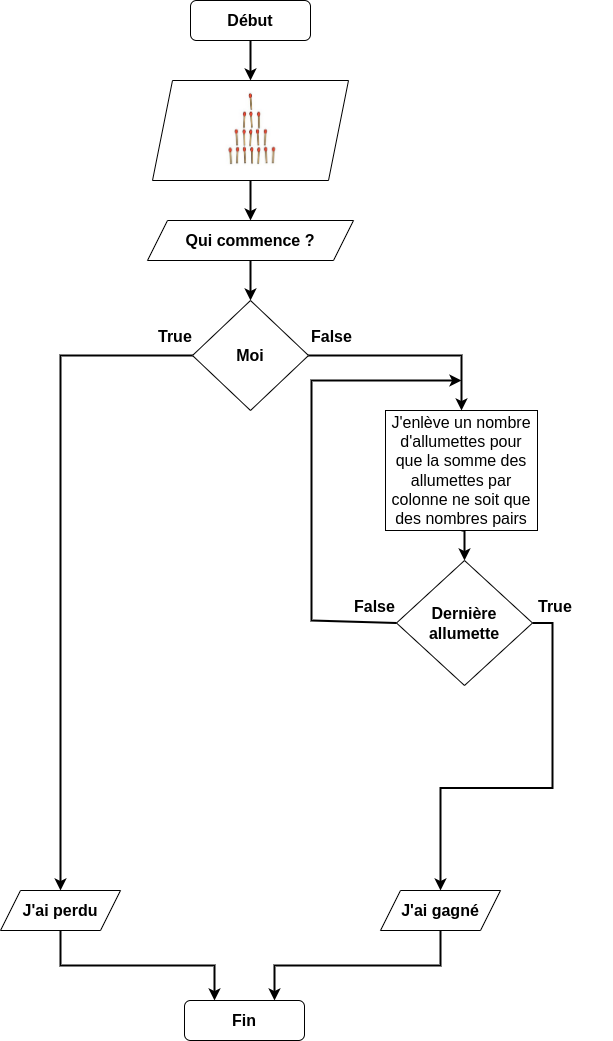
Dans le jeu de Marienbad, la stratégie gagnante est la suivante :
Toujours hériter d’une situation perdante
La transformer an une situation gagnante
Une situation gagnante se calcule simplement. Il faut additionner les nombre d’allumettes écrit en binaire mais osus forme dècimal.
Nombre d’allumettes |
Valeur en binaire |
|---|---|
1 |
|
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
Exemple, s’il reste 1 allumette sur la première rangée, 0 sur la seconde, 5 sur la troisième et 5 sur la dernière, on additionne :
001
000
101
101
===
203
Si tous les valeurs sont pair, alors la situation est gagnante. Sinon elle est perdante. Une situation gagnante ne peut pas retomber sur une situation gagnante. Quel que soit le coup, la situation suivante est perdante.