
TP1-REDO-03 : Types de fichiers et compression#
Objectifs pédagogiques#
Comprendre comment est construit un fichier en utilisant un éditeur hexadécimal
Comprendre le processus de compression sans perte avec le codage de Huffman
Être capable d’estimer la taille d’un fichier en fonction de son type et de son codage
PARTIE 2 : les fichiers informatiques#
Un fichier informatique est une séquence d’octets (de bits) qui représentent une information. Un fichier possède généralement :
un nom (par exemple
TravailDeMaturite)une extension qui est séparé du nom par un point
.(par exemple.docx,.pdf,.mp3)
Le fichier lui-même (ce qu’il contient) suit un format de fichier strict qui varie selon la représentation des données qu’il contient. Parfois cette représentation (le format) est ouvert (c’est le cas par exemple d’un fichier .pgm ou .ppm que l’on peut retrouver ici), parfois il est fermé (ou propriétaire) et ne peut être lu ou écrit uniquement par l’application propriétaire (par exemple .xls ou .doc qui appartiennent à l’entreprise Microsoft).
Plonger dans un fichier : éditer en hexadécimal#
Prise en main d’un éditeur hexadécimal
Découvrir que tous les fichiers sont faits de bytes
Découvrir les types de fichiers et le magic number
Comprendre le lien entre extension de fichier et programme qui va ouvrir le fichier
Découvrir quels types de fichiers sont robustes face a une modification / perturbation arbitraire.
Contexte#
Lorsqu’un fichier est enregistré sur un medium (un disque dur ou une clef USB par exemple), un lien est aussi créé et qui permet de relier son emplacement physique sur le disque (son adresse) à la liste affichée par un explorateur de fichiers (le Finder par exemple).
Imaginez-vous la situation suivante :
Un truand a enregistré ses complices, il a créé un dossier fichiers des fichiers texte contenant l’ensemble de ses contacts, il a même photographié l’arrivage de produit stupéfiants. Prévoyant, il en a créé une archive fichiers-zip en prenant garde d’enlever les suffixes de tous les fichiers ce qui les rend illisibles par son ordinateur.
Tous ces éléments sont compromettants.
Le truand a été dénoncé. Il voit arriver la police par sa fenêtre. Il a juste le temps de placer son dossier à la corbeille et d’appuyer sur vider la corbeille
Le policier scientifique c’est maintenant vous. Vous devez retrouver le contenu de tous les fichiers du truand.
Exercice 1#
Consignes#
Faites cet exercice par 2, sur un seul ordinateur, et discutez des résultats. A la fin, une discussion avec le reste du groupe où je vous demanderai ce que vous avez trouvé.
Dans le finder affichez les extensions de fichier :
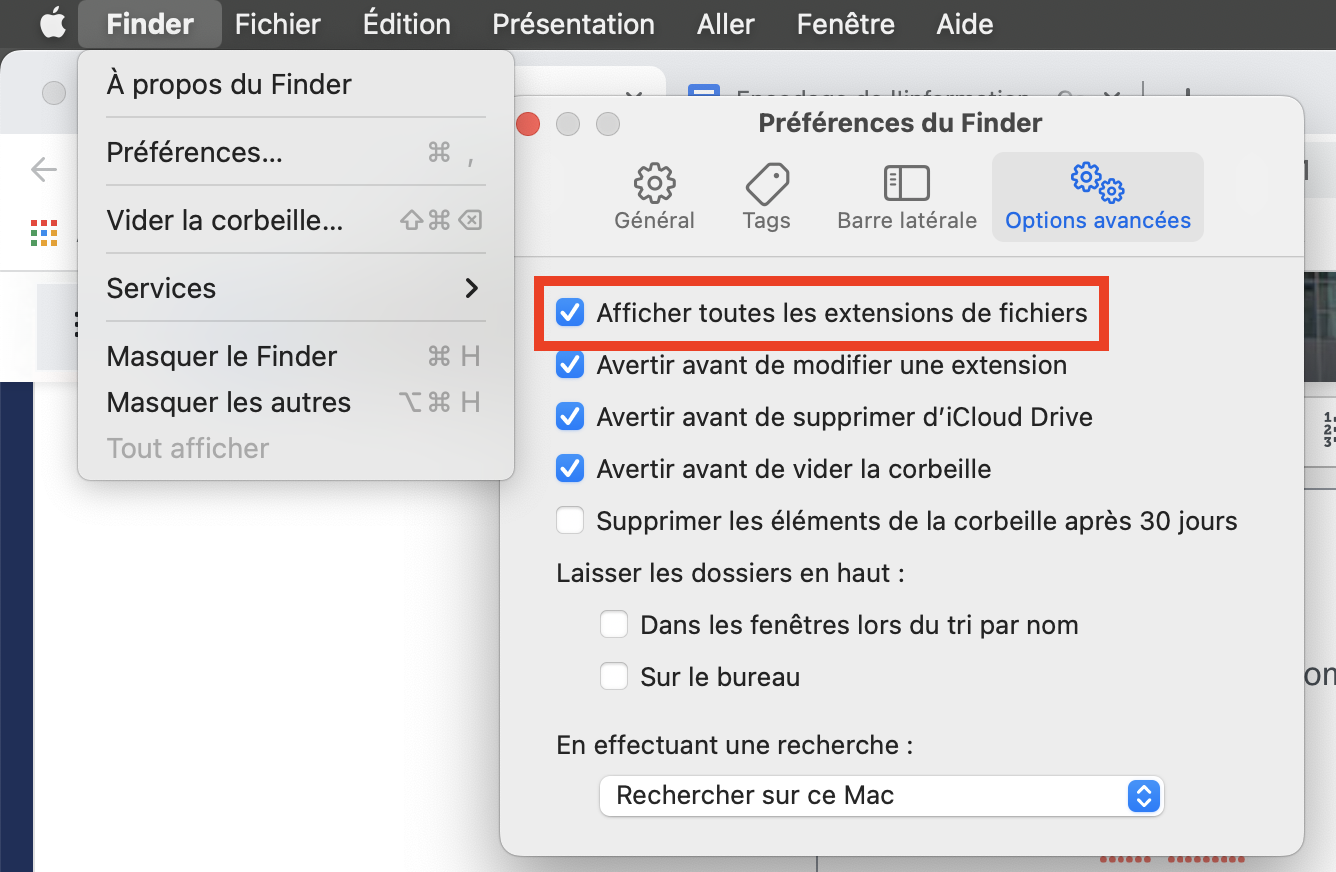
Téléchargez cette archive et décompressez-la
Pour chaque fichier:
Ouvrez le dans Hex Fiend
Essayez de déterminer de quel type de fichier il s’agit. Regardez vers le début du fichier. Si vous ne voyez pas immédiatement de quel type il pourrait choisir, aidez vous de cette page wikipédia : Nombre magique.
Renommez le fichier pour lui attribuer la bonne extension, par exemple fichier1.pptx
Double cliquez sur le fichier renommé pour vérifier si vous avez trouvé la bonne extension (si ça ne marche pas, c’est que vous n’avez pas le bon format ou la bonne extension)
Note : si un fichier est trop difficile à identifier, passez alors au suivant.
Ensuite, pour chaque fichier renommé :
Essayez d’éditer le contenu du fichier en remplaçant quelques bytes vers le milieu du fichier
Vérifiez ce qu’il se passe quand vous essayez maintenant d’ouvrir le fichier
Réessayez avec différents types de modifications
supprimer un peu ou beaucoup de bytes
dupliquer certaines parties 2, 3, 10 fois…
Notez ce qui se passe pour chaque type de fichier
Faites des suppositions sur pourquoi les différents types de fichiers réagissent différemment
A la fin : discussion avec le reste de la demi classe
Exercice 2 : manipuler du son#
Le format MP3 est un format de compression avec perte d’information. A l’origine, il a été développé pour la radiodiffusion (le streaming).
Téléchargez les trois fichiers son présent sur le git
A l’aide de HexFiend, identifiez le début et la fin de la musique
A l’aide des opérations de copie et coller, reproduisez le jingle francophone 3 fois.
Ouvrez les autres jingle (italophone et germanique) et créez un nouveau fichier contenant les trois à la suite à l’aide d’HexFiend
PARTIE 2 : Fichiers compressés#
On se rend vite compte que la quantité d’information contenue dans les fichiers peut rapidement prendre des grandes proportions. Vient alors l’idée d’analyser l’agencement des octets et bits et d’imaginer une façon de réduire leur nombre afin de gagner de la place, du temps de transmission et de l’efficacité.
Réduire la taille de l’information à transmettre tout en s’assurant que l’on peut retrouver tout ou partie de l’information est ce que l’on appelle compression de données.
Exemple !#
Laura a utilisé 26 lettres, 5 espaces et un emoji pour dire :
Je n’en peux plus ! Je suis dans le même état que Chrysippe de Soles, philosophe stoïcien du IIIème siècle avant Jésus-Christ après avoir vu un âne manger ses figues, mais la cause m’en a complètement échappé
qui est certes beaucoup plus poétique, mais qui prend 172 caractères, 36 espaces et des signes de ponctuation.
Définition : compression de donnée#
La compression de données est l’opération informatique \(C()\) qui consiste à faire passer une suite de bits \(X\) en en suite de bits \(Y < X\) :
L’opération inverse \(C^{-1}()\) est appelée décompression de données:
Il existe deux types de compressions de données :
La compression avec perte d’information qui ne permet pas de retrouver, après décompression, la suite de bits non-compressée
La compression sans perte d’information qui permet de retrouver, après décompression, l’entier de la suite de bits non-compressée
Compression avec perte d’information#
La compression avec perte d’information est une opération complexe qui dépasse le cadre de ce cours. Elle fait appel à des outils mathématiques qui ne sont pas traités dans le cadre des études gymnasiales.
(La compression avec perte d’information ne sera pas évaluée lors d’un test)
Compression sans perte d’information#
Il en existe plusieurs. Nous allons aborder le codage de Huffman.
Algorithme de Huffman#
Parmis les types de compression de donnée sans perte d’information, on trouve l’algorithme de Huffman. Il repose sur un modèle statistique.
Activité de magie#
Retrouver la lettre secrète.
Choisir une lettre parmi “ABCDEFGHIJKLMNOP”
poser des questions binaires pour la retrouver. Une question binaire est une question qui se répond uniquement par oui ou par non.
Combien de questions doit-on poser pour retrouver la lettre ?
Activité “Singing in the rain”#
Retrouver la lettre secrète plus rapidement.
choisir une lettre parmi la phrase “SINGING IN THE RAIN”
poser des questions binaires pour les retrouver.
Combien de questions doit-on poser ?
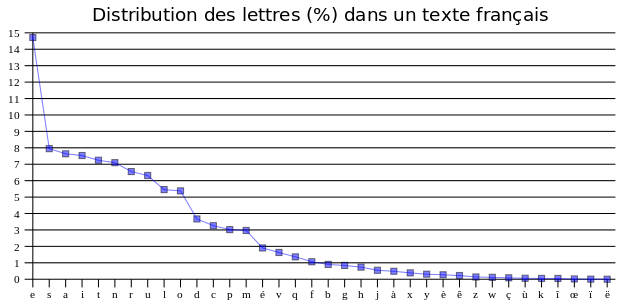
Codage de Huffmann#
Dans un premier temps, il faut observer que les lettres apparaissent suivant une distribution différente. On compte donc le nombre d’apparitions de chacune des lettres:
lettre |
I |
N |
G |
S |
T |
H |
E |
R |
A |
|---|---|---|---|---|---|---|---|---|---|
nombre d’apparitions |
4 |
4 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
Quelle est donc la première question à poser ?
Quelle est la seconde question à poser ?
On procède de la même manière en divisant les lettres (dans leur ordre d’apparition). On obtient donc un nombre de questions différentes en fonction du nombre d’apparitions :
lettre |
I |
N |
G |
S |
T |
H |
E |
R |
A |
|---|---|---|---|---|---|---|---|---|---|
nombre d’apparitions |
4 |
4 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
nombre de questions |
2 |
2 |
3 |
4 |
4 |
4 |
4 |
4 |
4 |
Finalement il faut encoder chaque lettre avec un nombre de bits variables.
Chaque lettre est encodée avec un nombre de bits égal au nombre de questions binaires nécessaires pour deviner la lettre.
Le mot de code associé à chaque lettre est la séquence de bits correspondant à la séquence de réponses obtenues lors du jeu (avec la correspondance oui=1 et non=0, par exemple).
Ainsi, on obtient :
lettre |
I |
N |
G |
S |
T |
H |
E |
R |
A |
|---|---|---|---|---|---|---|---|---|---|
nombre d’apparitions |
4 |
4 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
nombre de questions |
2 |
2 |
3 |
4 |
4 |
4 |
4 |
4 |
4 |
lettre encodée en binaire |
11 |
10 |
011 |
0101 |
0100 |
0011 |
0010 |
0001 |
0000 |
On appelle cet encodage un dictionnaire.
On observe finalement que la phrase “SINGING IN THE RAIN” s’encode par :
010111100111110011...
Si l’on lit cette séquence de gauche à droite, il y a toujours qu’une seule possibilité de décodage et donc on peut récupérer l’ensemble de la phrase.
Taux de compression#
Si l’on code les 16 lettres avec 4 bits, la phrase “SINGING IN THE RAIN” contient \(16 * 4 bits = 64 bits\). A l’aide du codage de Huffmann, on descend à \(46 bits\).
On peut donc calculer le taux de compression : \(\frac{64 - 46}{64} = \frac{18}{64} \approx 28 \%\)
Définition : Taille d’un fichier#
La taille d’un fichier mesure la quantité de données du fichier. Elle se mesure en octets (à laquelle on peut ajouter un suffixe). Alternativement, elle donne une idée de la quantité de stockage requise pour le stocker.
Suffixes pour les grandes valeurs#
Dans le Système international d’unités, il est d’usage d’utiliser des préfixes que l’on ajoute avant l’unité.
Ainsi :
Nom |
Symbole (fr/en) |
Valeur |
|---|---|---|
Kilooctet |
ko (kB) |
\(10^{3}\) octets = 8 kb |
mégaoctet |
Mo (MB) |
\(10^{6}\) octets = 8 Mb |
gigaoctet |
Go (GB) |
\(10^{9}\) octets = 8 Gb |
téraoctet |
To (TB) |
\(10^{12}\) octets = 8 Tb |
pétaoctet |
Po (PB) |
\(10^{15}\) octets = 8 Pb |
exaoctet |
Eo (EB) |
\(10^{18}\) octets = 8 Eb |
zettaoctet |
Zo (ZB) |
\(10^{21}\) octets = 8 Zb |
yottaoctet |
Yo (YB) |
\(10^{24}\) octets = 8 Yb |
Attention : lorsqu’on parle de capacité, on préférera le terme français “octet” plutôt que byte qui est phonétiquement trop proche de bit
Estimation de la taille d’un fichier#
Fichier texte ASCII#
On sait que chaque caractère ASCII est codé sur 7 bits. Mais un ordinateur ne travaille qu’avec des octets. Ainsi, en comptant le nombre de caractères d’un fichier, on peut estimer sa taille.
Téléchargez le fichier texte suivant
Terminal : dans un terminal, on peut utiliser la fonction wc qui donne le nombre exact de caractères d’un fichier. Par exemple : wc -c < AuClairDeLaLune.txt
Fichier image PPM et PGM#
Sur un fichier en niveaux de gris (PGM) et en couleurs (PPM), la taille du fichier peut être estimée avec la taille de l’image ainsi que le mode de codage des couleurs (\([0,1]\) pour \(P1\) donc 1 octet, \([0,...,255]\) pour \(P2\) donc 1 octet, \([0,...,255;0,...,255;0,...,255]\) pour \(P3\) donc 3 octets,
Fichier son#
Un fichier son non-compressé aura une taille multiple par la fréquence d’échantillonnage, la durée du morceau ainsi et le nombre de bits de la quantification.
Ressources supplémentaires#
from IPython.display import YouTubeVideo
YouTubeVideo('K2IQLk-BGuk', width=960, height=540)
