
TP2-ARCH-01 : Les portes logiques#
Objectifs pédagogiques#
Connaître les portes logiques
être capable de penser, dessiner et tester des circuits logiques simples
Couches d’abstractions architecturales#
Un ordinateur moderne fonctionne en binaire. Il ne connaît que deux valeurs définies : 1 pour vrai et 0 pour faux. Physiquement, les deux valeurs 0 (False), 1 (ou True) sont représentées par deux tensions électriques différentes : V0 et V1.
Ce TP se concentre sur des couches de plus bas niveau : à celui des circuits électroniques
Circuit électronique de test#
Lorsqu’on se situe dans les couches les plus basses de l’architecture d’un ordinateur, il est tout à fait possible de tester ses réalisations à l’aide d’un breadboard (une platine d’experimentation). C’est un outil qui permet de créer des prototypes de circuits électroniques et de les tester : il ne nécessite aucune soudure. Sur ce breadboard, on connecte les différents composants électroniques à l’aide de câbles de connexion. Une simple pile électrique fourni l’énergie.

Outil à disposition#
Ce TP sera effectué sur le logiciel de simulation logic. Les premiers exercices vous permettent de prendre en main le logiciel.
Il est toujours possible de sauvegarder son travail sous la forme d’un fichier json. Ce fichier peut ensuite être rechargé dans le même logiciel de simulation.
Définition : une porte logique#
Une porte logique est un composant électronique qui réalise des opérations logiques (algèbre de Boole). Une porte logique est désignée par l’opération logique qu’elle accomplit.
Elle possède une ou des entrées et des sorties et on les classe en fonction du nombre d’entrées.
Physiquement, une porte logique est un semi-conducteur piloté par une horloge.
Table de vérité#
Chaque porte logique est associée à une table de vérité. En fonction de l’entrée ou des entrées, on calcule la sortie avec l’opération logique qu’elle accomplit.
Par exemple : la fonction OR possède la table de vérité suivante :
a |
b |
a |
|---|---|---|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
Portes à une entrée#
NOT#
Symbole :#
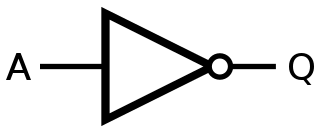
Table de vérité#
a |
|
|---|---|
0 |
1 |
1 |
0 |
BUFFER#
Symbole :#
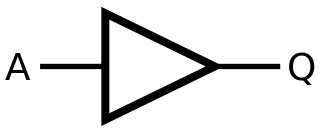
Table de vérité#
a |
|
|---|---|
0 |
0 |
1 |
1 |
Portes à deux entrées#
AND#
Symbole :#
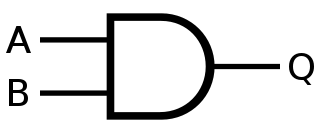
Table de vérité#
a |
b |
a |
|---|---|---|
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
NAND#
Symbole :#
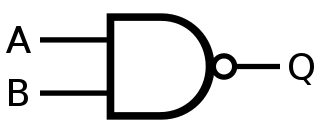
Table de vérité#
a |
b |
a |
|---|---|---|
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
OR#
Symbole :#
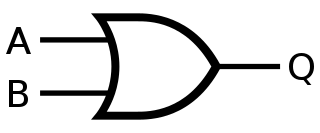
Table de vérité#
a |
b |
a |
|---|---|---|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
NOR#
Symbole :#
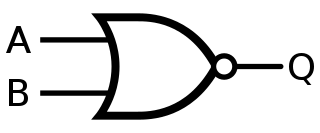
Table de vérité#
a |
b |
a |
|---|---|---|
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
XOR#
Symbole :#
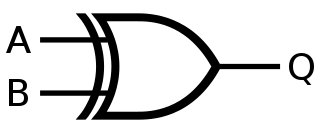
Table de vérité#
a |
b |
a |
|---|---|---|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
XNOR#
Symbole :#
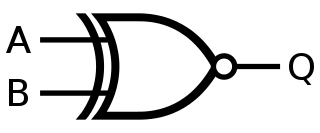
Table de vérité#
a |
b |
a |
|---|---|---|
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
Schéma électronique d’une porte NAND (exemple)#
Chaque porte logique peut être construite à l’aide de composants électroniques simples. Ici une porte NAND construite à l’aide de deux transistors et de quatre résistances
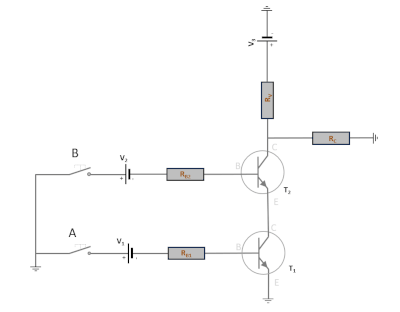
Source : https://electro-robot.com/les-activites/travaux-diriges-la-porte-logique-nand
Exercice 1 : Prise en main de l’outil#
Observez l’ensemble des éléments à disposition :
entrées et sorties
segments et afficheurs
horloge
portes logiques
composants logiques
Vérifiez la table de vérité d’une porte
ANDen créant :deux entrées
une sortie
des câbles de transmission
Modifiez à l’aide du menu contextuel (clic droit) la vitesse de transmission du signal dans le fil

Exercice 2 : Un sélecteur de chiens#
La famille Dupont a décidé d’accueillir un chien à la maison et se rend dans un refuge SPA afin d’en choisir un.
Chaque chien a des caractéristiques propres. Afin de ne pas perdre trop de temps au refuge, la famille Dupont a décidé d’amener un petit circuit électronique qui sera capable d’identifier immédiatement si un chien convient à ses exigences, en fonction de ses caractéristiques.
Réfléchissez à la manière de construire ce circuit électronique.
Ex 2.1 : Petit et gentil#
Toute la famille est d’accord : le chien devra être petit et gentil .
Ecrivez la table de vérité du circuit que vous voulez implémenter
A l’aide du simulateur, développez un circuit qui répond à cette question.
deux entrées : gentil et petit
une sortie : OK
Ex 2.2 : Et s’il bave tout le temps ?#
La famille Dupont est unanimement d’accord, si le chien bave tout le temps c’est rédhibitoire et le chien ne peut pas être accepté.
Ecrivez la table de vérité du circuit que vous voulez implémenter
Sur le circuit 2.2, ajoutez :
une entrée : bave tout le temps
vérifiez la validité du circuit
Truc : vous devrez utiliser une seconde porte logique à une seule entrée
Ex 2.3 : Papa, Maman, … j’veux un Labrador !!#
La petite dernière de la famille Dupont aime particulièrement les Labrador. Or les Labrador ne sont pas des petits chiens. La famille se met d’accord pour une exception : le chien doit être petit sauf si c’est un Labrador.
Ecrivez la table de vérité du circuit que vous voulez implémenter (16 entrées !!!)
Sur le circuit 2.2, ajoutez :
une entrée Labrador
vérifiez la validité du circuit (il n’y a pas qu’une seule solution)
Attention : un Labrador n’est pas un petit chien !
Un gentil Chihuahua qui ne bave pas est-il un candidat ?
Un gentil Saint-Bernard qui bave est-il un candidat ?
Exercice 3 : Le refuge de la SPA#

Le refuge de la SPA est divisé en 4 secteurs qui abritent 4 races de chiens. Chaque secteur a droit à une promenade à un moment différent de la journée. Le refuge de la SPA souhaite créer un système électronique pour ouvrir les portes au bon moment de la journée à partir du numéro du secteur.
Ex 3.1 Combien de bits ?#
combien de bits sont nécessaire pour coder les 4 secteurs ?
Ex 3.2 Un décodeur électronique#
Voici les 4 races de chiens correspondant aux 4 secteurs :
Secteur |
Race |
|---|---|
0 |
Pittbulls |
1 |
Pyrénées |
2 |
Dalmatiens |
3 |
Labradors |
Codez le numéro des secteurs
Construisez un décodeur avec le nombre d’entrées correspondant au nombre de bits nécessaires et qui active une seule des 4 sorties (le numéro du secteur) à la fois.
vous pouvez vous aider d’une table de vérité
Exercice 4 : Et la famille Rochat ?#
La famille Rochat a construit un circuit similaire pour le choix de son chien. Le voici :
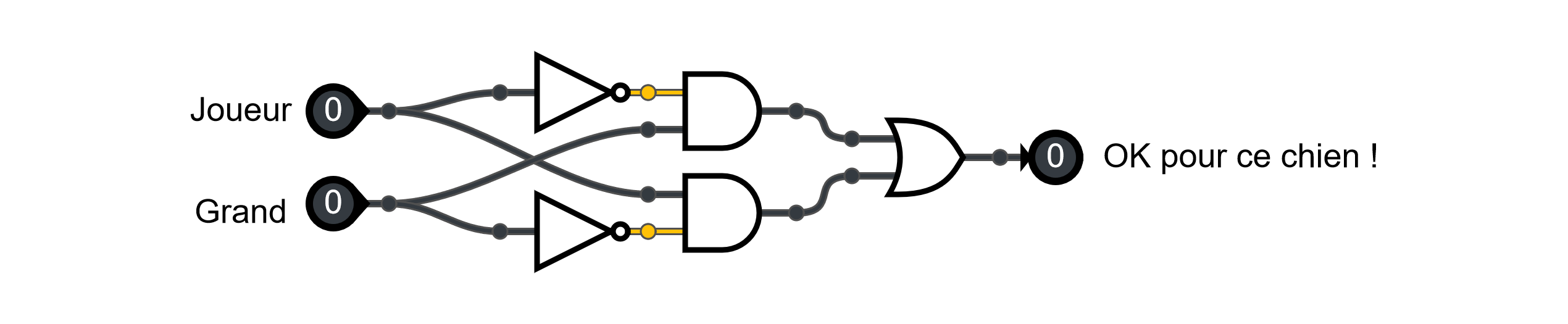
Quels sont les critères de la famille Rochat ?
Testez avec le simulateur logique
Est-il possible de créer le même circuit électronique avec seulement 1 porte ?
Dessinez la table de vérité du circuit
Exercice 5 : Le coffre-fort#

Pour des raisons de sécurité, ce coffre-fort ne s’ouvre que si deux conditions sont remplies simultanément :
La clé physique est insérée (entrée K)
L’empreinte digitale est reconnue comme valide (entrée E)
Si la clé est présente mais que l’empreinte est refusée → une alarme se déclenche (tentative d’intrusion). Si la clé n’est pas présente → rien ne se passe (ni ouverture, ni alarme).
Consigne : Ecrire la table de vérité et construire le circuit logique
Exercice 6 : La banque#

Une banque sécurise son coffre avec trois responsables :
Alice : cheffe de caisse
Bernard : directeur adjoint
Carole : directrice
Règles de sécurité :
Le coffre s’ouvre si au moins deux responsables sont présents (principe de collégialité).
Une alarme silencieuse se déclenche si seul Bernard est présent (tentative suspecte : il n’a pas l’habitude d’agir seul).
Un verrouillage temporaire s’active si Alice seule est présente (mesure anti-usurpation : elle ne peut pas agir sans supervision).
Carole seule peut ouvrir le coffre (privilège hiérarchique).
Consigne : Ecrire la table de vérité et construire le circuit logique
Exercice 7 : Un demi-additionneur (pour aller plus loin)#
Un additionneur est un circuit logique permettant de réaliser une addition. En binaire, une addition sur un bit respecte la table de vérité suivante :
a |
b |
a \(\oplus\) b = s |
|---|---|---|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
La valeur s représente la somme des deux bits. A l’aide de portes logiques, construisez un circuit permettant l’addition de deux bits. On appelle ce circuit un demi-additionneur puisque la retenue r n’est pas calculée.
Exercice 8 : Un additionneur complet sur 1 bit#
Un additionneur complet nécessite une entrée supplémentaire : la retenur de l’addition précédente. Tout l’intérêt ici est de pouvoir chaîner plusieurs additionneurs complets à la suite.
La table de vérité d’un additionneur complet respecte la table de vérité suivante :
a |
b |
\(c_{in}\) |
a \(\oplus\) b = s |
\(c_{out}\) |
|---|---|---|---|---|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
Construisez un circuit logique permettant l’addition de deux bits avec retenue entrante (\(c_{in}\)) et retenue sortante (\(c_{out}\)). C’est l’additionneur complet sur 1 bit
Exercice 9 : Un additionneur complet sur 4 bits#
Chaînez 4 additionneurs complets pour effectuer des additions de nombres de 4 bits. Vous pouvez utiliser un Afficheur (dans les entrées sorties) qui permet d’afficher la valeur sur 4 bits en binaire et en décimal
Exercice 10 : comparateur#
Construisez un schéma avec les portes logiques qui doit :
avoir deux entrées (deux bits)
avoir trois sorties : I, E et S pour Inférieur, Egal et Supérieur
Le circuit doit comparer les deux bits d’entrée
