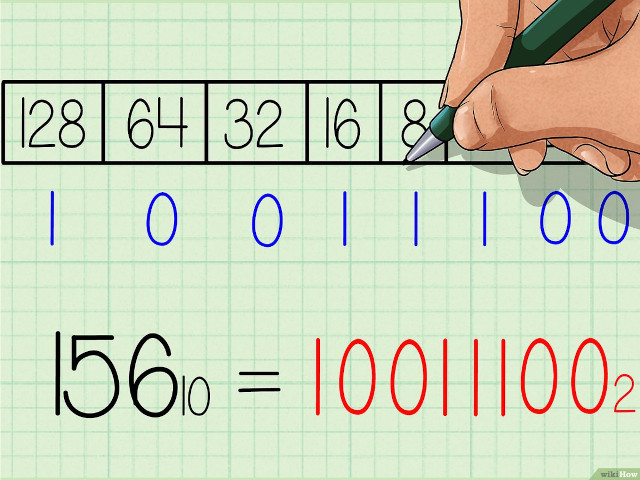
C1-REDO-03 : Opérations en binaire#
Objectifs pédagogiques#
réviser les conversion de bases 2, 10 et 16
être capable d’exécuter les opérations suivantes en binaire et en héxadécimal:
addition
soustraction
multiplication
division
Convention : les bases en indices#
Par convention, nous plaçons la base du nombre entier en indice de celui-ci :
\(100_{10}\) signifie le nombre 100 en base 10
\(100_{2}\) signifie le nombre 100 en base 2
\(100_{16}\) signifie le nombre 100 en base 16
Valeur décimale |
Valeur binaire |
valeur héxadécimale |
|---|---|---|
\(100_{10}\) |
\(1100100_{2}\) |
\(64_{16}\) |
\(4_{10}\) |
\(100_{2}\) |
\(4_{16}\) |
\(256_{10}\) |
\(100000000_{2}\) |
\(100_{16}\) |
Opérations algébriques en binaire#
Les 4 opérations de base en algèbre sont :
l’addition (signe \(+\))
la soustraction (signe \(-\))
la multiplication (signe \(*\))
la division (signe \(/\))
Addition#
Tout comme l’addition décimale, l’addition en binaire se fait en colonne et en utilisant les retenues (binaires !).
Il existe quatre possibilités d’additionner deux bits (ce sont les 4 règles de base de l’addition binaire :
\(0_{2} + 0_{2} = 0_{2}\)
0 |
||
+ |
0 |
|
— |
— |
— |
0 |
\(0_{2} + 1_{2} = 1_{2}\)
0 |
||
+ |
1 |
|
— |
— |
— |
1 |
\(1_{2} + 0_{2} = 1_{2}\)
1 |
||
+ |
0 |
|
— |
— |
— |
1 |
\(1_{2} + 1_{2} = 10_{2}\)
1 |
||
|---|---|---|
1 |
||
+ |
1 |
|
— |
— |
— |
1 |
0 |
Tout comme en décimal, on utilise la retenue pour ajouter un \(1_{2}\) sur la colonne suivante
Exemple : \(1010_{2} + 0011_{2}\)
1 |
|||
|---|---|---|---|
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
— |
— |
— |
— |
1 |
1 |
0 |
1 |
Exercice 1 : Addition en binaire#
Sur une feuille de papier, calculez le résultat des additions binaires suivantes :
\(1011_{2} + 1011_{2}\)
\(11110_{2} + 10011_{2}\)
\(101_{2} + 11_{2}\)
Soustraction#
Dans la soustraction binaire, on procède comme en décimal. Lorsque la quantité à soustraire est supérieure à la quantité dont on soustrait, on emprunte 1 au voisin de gauche.
Il existe quatre possibilités de soustraire 2 bits (ce sont les 4 règles de base de la soustraction binaire)
\(0_{2} - 0_{2} = 0_{2}\)
0 |
||
- |
0 |
|
— |
— |
— |
0 |
\(1_{2} - 0_{2} = 1_{2}\)
1 |
||
- |
0 |
|
— |
— |
— |
1 |
\(1_{2} - 1_{2} = 0_{2}\)
1 |
||
- |
1 |
|
— |
— |
— |
0 |
Tout comme en décimal, on utilise la retenue pour ajouter un \(1_{2}\) sur la colonne suivante
\(0_{2} - 1_{2} = 1_{2}\)
0 |
||
- |
1 |
|
— |
— |
— |
1 |
Attention, il y a un emprunt dans la colonne de gauche
Exemple : \(11011_{2} - 1101_{2}\)
0 |
0 |
||||
|---|---|---|---|---|---|
1 |
1 |
0 |
1 |
1 |
|
- |
1 |
1 |
0 |
1 |
|
— |
— |
— |
— |
— |
— |
0 |
1 |
1 |
1 |
0 |
On peut vérifier en décimal : \(27_{10} - 13_{10} = 14_{10}\)
Soustraction avec complément à 2#
L’électronique de l’ordinateur (voir cours + TP d’architecture des ordinateurs) peut additionner très simplement. La méthode de la soustraction binaire avec complément à 2 utilise ce principe. L’algorithme se décline en 5 étapes :
Aligner les deux nombres à soustraire sur le même nombre de bits
Prendre le complément à 2 du soustracteur : inverser tous les bits (le \(0\) devient un \(1\) et vice-versa)
Ajouter \(1\) à ce nombre binaire (en utlisant l’addition binaire)
Additionner les deux nombres. Si le bit de poids le plus fort (la retenue) dépasse la longueur du nombre de bits, alors il est ignoré
Exemple : \(11011_{2} - 1101_{2}\)
\(11011_{2} - 01101_{2}\)
Calculer le complément à 2 de \(01101_{2}\) : \(10010_{2}\)
Ajouter 1 au complément : \(10010_{2} + 00001_{2} = 10011_{2}\)
Additionner les deux nombres
1 |
1 |
1 |
||||
|---|---|---|---|---|---|---|
1 |
1 |
0 |
1 |
1 |
||
+ |
1 |
0 |
0 |
1 |
1 |
|
— |
— |
— |
— |
— |
— |
— |
1 |
0 |
1 |
1 |
1 |
0 |
Le bit de poids le plus fort (\(1\) tout à gauche) est laissé de côté puisqu’il se trouve en 6ème position. Résultat : \(01110_{2}\)
Exercice 2 : Soustraction binaire#
A l’aide de l’une des deux méthodes (méthode standard ou méthode du complément à 2), faites les calculs suivants :
\(1101_{2} - 0110_{2}\)
\(101101_{2} - 10110_{2}\)
\(10110_{2} - 1110_{2}\)
Multiplication#
La multiplication binaire n’est rien d’autre qu’une addition binaire.
Il existe quatre possibilités de multiplier 2 bits (ce sont les 4 règles de base de la multiplication binaire)
\(0_{2} * 0_{2} = 0_{2}\)
0 |
||
* |
0 |
|
— |
— |
— |
0 |
\(1_{2} * 0_{2} = 0_{2}\)
1 |
||
* |
0 |
|
— |
— |
— |
0 |
\(0_{2} * 1_{2} = 0_{2}\)
0 |
||
* |
1 |
|
— |
— |
— |
0 |
\(1_{2} * 1_{2} = 1_{2}\)
1 |
||
* |
1 |
|
— |
— |
— |
1 |
On procède exactement de la même manière que lors d’une multiplication décimale avec les retenues.
Exemple : \(1010_{2} * 101_{2}\)
1 |
||||||
|---|---|---|---|---|---|---|
1 |
0 |
1 |
0 |
|||
* |
0 |
1 |
0 |
1 |
||
— |
— |
— |
— |
— |
— |
— |
1 |
0 |
1 |
0 |
|||
0 |
0 |
0 |
0 |
|||
+ |
1 |
0 |
1 |
0 |
||
— |
— |
— |
— |
— |
— |
— |
1 |
1 |
0 |
0 |
1 |
0 |
Vérification en décimal : \(10_{10} * 5_{10} = 50_{10}\)
Exercice 3 : Multiplication binaire#
Faites les calculs suivants en utilisant la méthode de la multiplication binaire (les additions) :
\(1011_{2} * 111_{2}\)
\(1111_{2} * 1101_{2}\)
\(101_{2} * 1100_{2}\)
Division#
Tout comme la multiplication, la division binaire est une suite de soustractions (et donc d’additions au complément à 2 si l’on utilise cette méthode).
La division binaire se fait exactement comme la division décimale aprise à l’école primaire : avec la méthode dite de la potence
Prenons l’exemple décimal \(4356_{10} / 20_{10} = 217_{10}\) avec un reste de \(16_{10}\)
4356 │ 20
- 40 ├───────
──── │ 217
35 │
- 20 │
──── │
156 │
- 140 │
──── │
16 │
En division binaire, on procède de la même façon : analyse des chiffres et voir combien de fois on peut mettre le diviseur. Seule différence :
Si on peut diviser (division entière) le nombre, alors on met 1 au quotient,
sinon 0
Prenons un exemple : \(10111_{2} / 11_{2}\)
10111 │ 11
11 ├───────
──── │ 0111
010 │
- 11 │
──── │
0101 │
- 11 │
──── │
010 │
\(10111_{2} / 11_{2} = 0111_{2}\) avec un reste de \(010_{2}\) (On a bien que \(23_{10} / 3_{10} = 7_{10}\) avec un reste de \(2_{10}\)).
Remarque : il est tout à fait possible d’effectuer la soustraction en utilisant la méthode de l’addition du complément à 2.
Exercice 4 : Division binaire#
Faites les calculs suivants en utilisant la méthode de la potence :
\(1011010 / 10\)
\(111010 / 101\)
\(111111 / 11\)
Conclusion#
En binaire, toutes les opérations se résument à l’addition et quelques opérations sur les bits (comme dans le complément à 2 pour la soustraction). On peut essayer de résumer dans un tableau :
Opération |
en binaire, remplacée par |
remarques |
|---|---|---|
Addition |
Addition |
|
Soustraction |
Addition |
inversion des bits et addition de 1 (complément à 2) |
Multiplication |
Addition |
|
Division |
Addition |
En fait une soustraction qui se remplace par l’addition avec le complément à 2 |
Electroniquement, cela signifie que l’on peut construire une calculatrice à l’aide d’un circuit qui ne sait faire que les additions.
Au-delà des entiers (pour aller plus loin)#
De \(\mathbb{N}\) vers \(\mathbb{Z}\)#
Que vaut le résultat de l’opération suivante ?
\(00001000_{2} - 00010000_{2}\)
Un nombre entier (\(\mathbb{N}\)) ne peut pas être négatif. Le résultat de l’opération est \(-8_{10}\) et c’est un nombre relatif (\(\mathbb{Z}\)) . Il s’agit donc de trouver un système pour représenter les nombres négatifs. Le plus communément utilisé est le complément à 2
Ainsi, le nombre \(-5_{10}\) s’écrit en binaire :
Valeur absolue \(5_{10} = 00000101_{2}\)
Inversion des bits : \(11111010_{2}\)
Ajouter \(1_{10}\) : \(11111011_{2}\)
Donc \(-5_{10}\) en complément à 2 sur un octet vaut \(11111011_{2}\).
Trois propriétés importantes de cette notation :
le bit de poids le plus fort (celui qui se trouve le plus à gauche) donne le signe : \(0\) alors c’est un nombre positif, \(1\) c’est un nombre négatif
L’intervalle des nombres représentables sur \(n\) bits en complément à 2 est de \([-2^{n-1}, ..., 2^{n-1} -1]\)
L’addition fonctionne sans modification
De \(\mathbb{N}\) vers \(\mathbb{Q}\)#
Que vaut le résultat de l’opération suivante ?
\(00000101 / 00000010\)
Un nombre entier (\(\mathbb{N}\)) ne peut pas être rationnel. Le résultat de l’opération est \(2.5_{10}\) et c’est un nombre rationnel (\(\mathbb{Q}\)). Il s’agit de trouver une représentation pour les nombres rationnels (ou nombres à virgule). Il en existe deux:
La représentation à virgule fixe
La représentation à virgule flottante
Ces représentations vont au-delà du cadre de ce cours et seront abordé en 2ème année de l’école de maturité.
Rappel : Notation de droite à gauche#
La position du chiffre correspond à la puissance de la base.
Base 10 (décimal)#
En décimal, il existe 10 symboles pour écrire les nombres entiers : \([0,1,2,3,4,5,6,7,8,9]\). Ainsi :
position |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
|---|---|---|---|---|---|---|---|---|
puissance |
\(10^7\) |
\(10^6\) |
\(10^5\) |
\(10^4\) |
\(10^3\) |
\(10^2\) |
\(10^1\) |
\(10^0\) |
décimal |
\(10000000_{10}\) |
\(1000000_{10}\) |
\(100000_{10}\) |
\(10000_{10}\) |
\(1000_{10}\) |
\(100_{10}\) |
\(10_{10}\) |
\(1_{10}\) |
Ainsi, le nombre \(2017\) lu de droite à gauche se calcule : \(7*10^{0} + 1*10^{1} + 0*10^{2} + 2*10^{3} = 7 + 10 + 0 + 2000 = 2017\)
Base 2 (binaire)#
En binaire, il existe 2 symboles pour écrire les nombres entiers : \([0,1]\).
position |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
|---|---|---|---|---|---|---|---|---|
puissance |
\(2^7\) |
\(2^6\) |
\(2^5\) |
\(2^4\) |
\(2^3\) |
\(2^2\) |
\(2^1\) |
\(2^0\) |
binaire |
\(10000000_{2}\) |
\(1000000_{2}\) |
\(100000_{2}\) |
\(10000_{2}\) |
\(1000_{2}\) |
\(100_{2}\) |
\(10_{2}\) |
\(1_{2}\) |
décimal |
\(128_{10}\) |
\(64_{10}\) |
\(32_{10}\) |
\(16_{10}\) |
\(8_{10}\) |
\(4_{10}\) |
\(2_{10}\) |
\(1_{10}\) |
Ainsi, le nombre \(10101101\) lu de droite à gauche se calcule en base 10 : \(1_{2}*2_{10}^{0} + 0_{2}*2_{10}^{1} + 1_{2}*2_{10}^{2} + 1_{2}*2_{10}^{3} + 0_{2}*2_{10}^{4} + 1_{2}*2_{10}^{5} + 0_{2}*2_{10}^{6} + 1_{2}*2_{10}^{7} = 1_{10} + 0_{10} + 4_{10} + 8_{10} + 0_{10} + 32_{10} + 0_{10} + 128_{10} = 173_{10}\)
Le bit le plus à droite s’appelle bit de poids faible
Le bit le plus à gauche s’appelle bit de poids fort
Base 16 (hexadécimal)#
En héxadécimal, il existe 16 symboles pour écrires les nombres entiers : \([0,1,2,3,4,5,6,7,8,9, A, B, C, D, E, F]\). Puisque \(16_{10} = 2_{10}^{4}\) il faut quatre bits pour convertir un nombre héxadécimal en binaire.
Valeur décimale |
Valeur binaire |
valeur héxadécimale |
|---|---|---|
\(0_{10}\) |
\(0000_{2}\) |
\(0_{16}\) |
\(1_{10}\) |
\(0001_{2}\) |
\(1_{16}\) |
\(2_{10}\) |
\(0010_{2}\) |
\(2_{16}\) |
\(3_{10}\) |
\(0011_{2}\) |
\(3_{16}\) |
\(4_{10}\) |
\(0100_{2}\) |
\(4_{16}\) |
\(5_{10}\) |
\(0101_{2}\) |
\(5_{16}\) |
\(6_{10}\) |
\(0110_{2}\) |
\(6_{16}\) |
\(7_{10}\) |
\(0111_{2}\) |
\(7_{16}\) |
\(8_{10}\) |
\(1000_{2}\) |
\(8_{16}\) |
\(9_{10}\) |
\(1001_{2}\) |
\(9_{16}\) |
\(10_{10}\) |
\(1010_{2}\) |
\(A_{16}\) |
\(11_{10}\) |
\(1011_{2}\) |
\(B_{16}\) |
\(12_{10}\) |
\(1100_{2}\) |
\(C_{16}\) |
\(13_{10}\) |
\(1101_{2}\) |
\(D_{16}\) |
\(14_{10}\) |
\(1110_{2}\) |
\(E_{16}\) |
\(15_{10}\) |
\(1111_{2}\) |
\(F_{16}\) |
Exercice 5 : Conversion binaire - décimal - héxadécimal#
Complétez le tableau suivant. Lorsque le nombre de bits n’est pas divisible par 4 en binaire, ajoutez des \(0\) sur les bits de poids le plus fort (à gauche) pour complèter au multiple.
Valeur binaire |
Valeur décimale |
valeur héxadécimale |
|---|---|---|
\(11010101_{2}\) |
||
\(1984_{10}\) |
||
\(BEEF_{16}\) |
||
\(51966_{10}\) |
||
\(100101110_{2}\) |
