C2-ALGO-04-A : Introduction à la théorie des graphes#
Objectifs pédagogiques#
connaître les différentes utilisation des graphes dans l’informatique
connaître la définition d’un graphe
être capable de construire et lire une matrice d’adjacence
appliquer l’algorithme de Dijkstra du plus court chemin sur un graphe
Exemple introductif#
Il est d’usage d’introduire la théorie des graphes en présentant le célèbre problème dit des sept ponts de Königsberg.
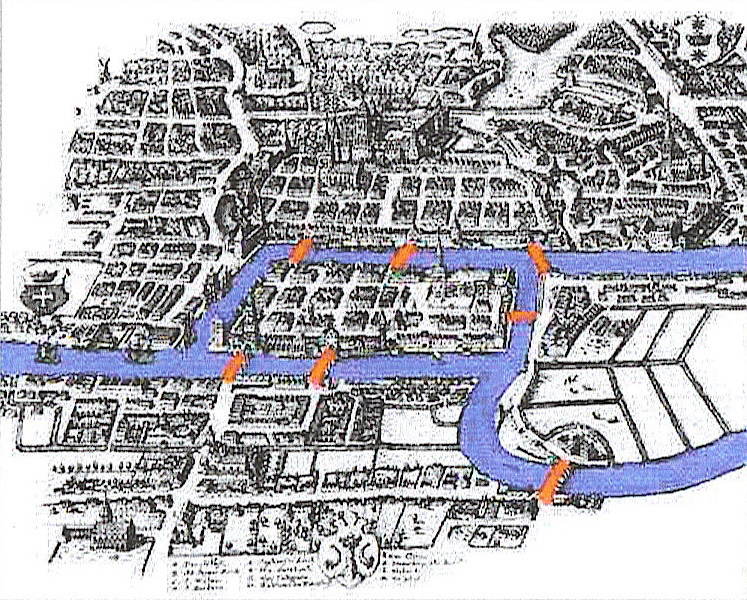
Le problème est le suivant : La ville de Königsberg (aujourd’hui Kaliningrad), du temps de Leonhard Euler le célèbre mathématicien et physicien suisse qui l’a résolu, est construite dans l’estuaire du fleuve Pregolia sur 5 îles reliées par des ponts. Ces ponts étaient au nombre de 7 du temps d’Euler. Le problème consiste à partir d’un point de départ au choix, de passer une et une seule fois sur chacun des sept ponts et à revenir au point de départ.
Solution : il n’existe pas de solution à ce problème. La démonstration (faite par Euler) dépasse largement le cadre de ce cours d’informatique
Utilisation des graphes#
Les graphes sont utilisés dans divers domaines :
Les réseaux informatiques
Les réseaux sociaux
La cartographie
Les réseaux de neurones (et donc l’IA)
Quelques exemples#
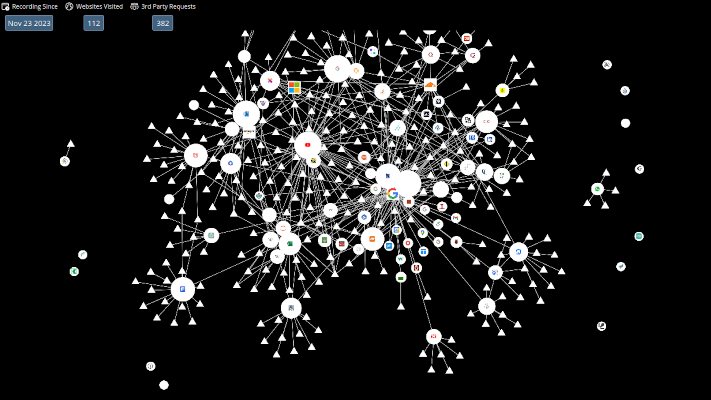
Les réseaux informatiques#
L’image ci-dessous représente le graphe des requêtes vers les sites tiers ainsi que les cookies déposés par ces derniers avec lesquels l’internaute a interagi. Il s’agit d’une extension libre du navigateur libre Firefox
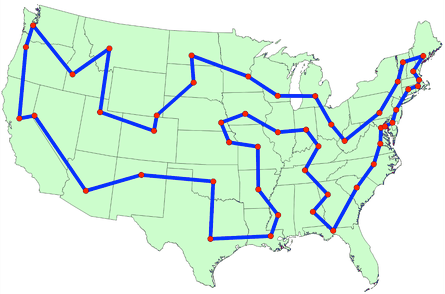
La cartographie#
L’image ci-dessous représente une solution du célèbre problème du voyageur de commerce (Travaling Salesman Problem). L’idée est de trouver le chemin le plus court qui passe une seule fois par chacun des sommets (représentant ici les capitales des états amércains)
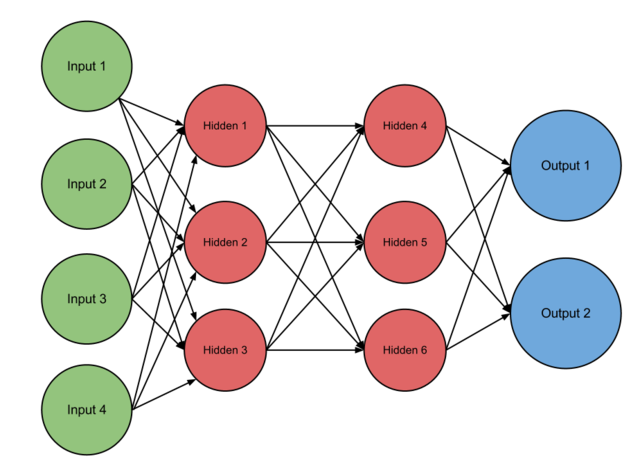
Les réseaux de neurones#
L’image ci-dessous représente un réseau de neurones artificielles, l’un des composants de base vers la créations d’une intelligence artificielle.
Définition : graphe#
Un graphe est une structure composée de deux objets :
Une liste de sommets. Un sommet peut avoir un nom
Une liste d’arêtes qui relient les sommets.
La représentation courante est graphique avec des cercles pour les sommets et des lignes pour les arêtes.
Définition : graphe orienté#
les arêtes peuvent avoir un sens d’un sommet à un autre. On les représente avec des flèches et une direction. L’arête devient alors un arc
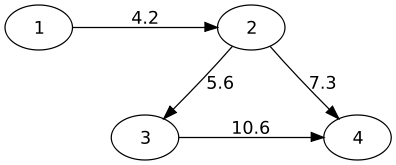
On parle alors d’un graphe orienté
Définition : graphe pondéré#
Une arête (ou un arc) peut possèder un poids qui représente n’importe quelle grandeur (une longueur, un coût, etc..)
On parle alors de graphe pondéré
Définition : boucle#
Lorsqu’une une arête ou un arc relie un sommet à lui-même, on parle d’une boucle
Exemple : une carte de métro#
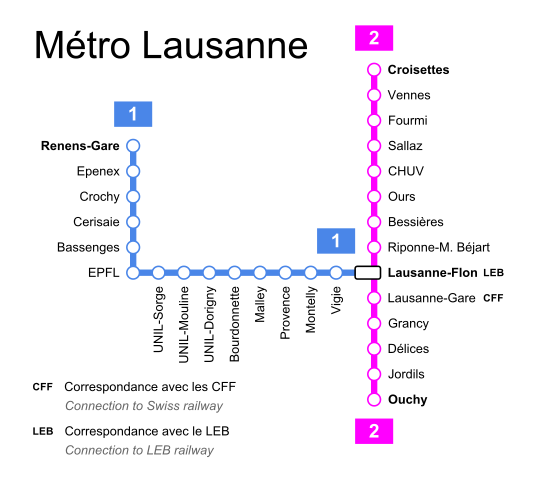
Le plan des deux lignes de métro de Lausanne est un graphe.
Que sont les sommets ?
Que sont les arêtes ?
Le graphe est-il orienté ? Pondéré ? Si non, que faudrait-il ajouter pour l’orienter ? Pour le pondérer ?
Peut-on en faire de même avec le plan du métro de Tokyo ?
Définition : matrice d’adjacence#
Lorsque le graphe est trop complexe pour être représenté graphiquement, on utilise un tableau. En mathématique, on parle de matrice.
Une matrice d’adjacence pour un graphe à n sommets est un tableau de dimension n x n dont chaque élément qui ne se trouve pas sur la diagonale contient le poids de l’arête qui relie les deux sommets à l’intersection de la colonne et de la ligne. Si les arêtes ne possèdent pas de poids, alors on indiquera 1 si une arête existe, 0 sinon.
Exemple#
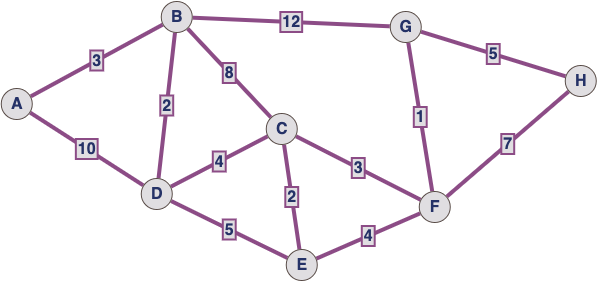
La matrice d’adjacence se présente alors ainsi :
A |
B |
C |
D |
E |
F |
G |
H |
|
|---|---|---|---|---|---|---|---|---|
A |
3 |
0 |
10 |
0 |
0 |
0 |
0 |
|
B |
3 |
8 |
0 |
0 |
0 |
12 |
0 |
|
C |
0 |
8 |
4 |
2 |
3 |
0 |
0 |
|
D |
10 |
0 |
4 |
5 |
0 |
0 |
0 |
|
E |
0 |
0 |
2 |
5 |
4 |
0 |
0 |
|
F |
0 |
0 |
3 |
0 |
4 |
1 |
7 |
|
G |
0 |
12 |
0 |
0 |
0 |
1 |
5 |
|
H |
0 |
0 |
0 |
0 |
0 |
7 |
5 |
Mathématiquement on la présente ainsi :
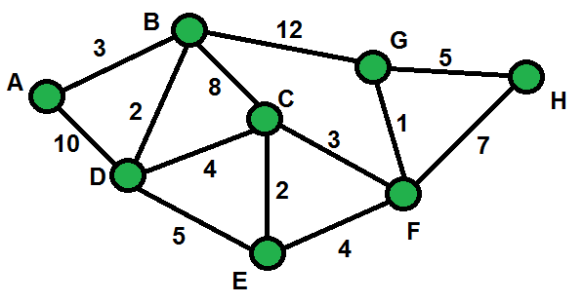
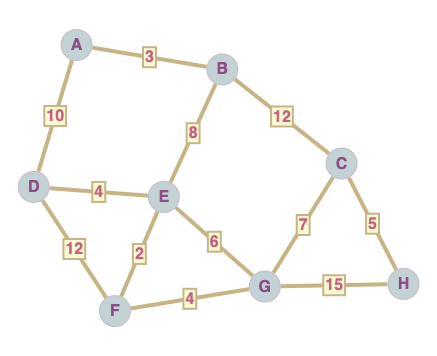
Exercice 1 : matrice d’adjacence#
Ecrivez la matrice d’adjacence du graphe suivant :
Cas d’usage de la matrice d’adjacence#
La matrice d’adjacence, contrairement au graphe “visuel”, permet d’identifier de nombreux éléments très rapidement
Voisins d’un sommet#
Les réseaux sociaux utilisent ce cas d’usage. Dans un réseau social, chaque personne (profil) est un sommet d’un très grand graphe représenté par une matrice d’adjacence. Une arête relie deux sommet si ces personnes sont amies.
Ainsi, l’utilité de la matrice d’adjacence permet d’identifier immédiatement avec qui une personne est amie. Une ligne (ou une colonne) représente un profil, il est très rapide de savoir qui est connecté avec qui.
A B C D
A 0 1 0 1
B 1 0 1 0
C 0 1 0 1
D 1 0 1 0
Ici, A est connecté avec B et D.
Programmation#
Lorsqu’on programme un réseau social, un système GPS ou n’importe quel algorithme qui demande un graphe, il est très facile de représenter ce graphe en mémoire avec la matrice d’adjacence directement : c’est un simple tableau 2D.
A = [0,3,0,10,0,0,0,0]
B = [3,0,12,0,8,0,0,0]
C = [0,12,0,0,0,0,7,5]
D = [10,0,0,0,4,12,0,0]
E = [0,8,0,4,0,2,6,0]
F = [0,0,0,12,2,0,4,0]
G = [0,0,7,0,6,4,0,15]
H = [0,0,5,0,0,0,15,0]
graphe = [A,C,D,E,F,G,H]
i = 0
while i < 7 :
print(graphe[i])
i = i + 1
[0, 3, 0, 10, 0, 0, 0, 0]
[0, 12, 0, 0, 0, 0, 7, 5]
[10, 0, 0, 0, 4, 12, 0, 0]
[0, 8, 0, 4, 0, 2, 6, 0]
[0, 0, 0, 12, 2, 0, 4, 0]
[0, 0, 7, 0, 6, 4, 0, 15]
[0, 0, 5, 0, 0, 0, 15, 0]
Avec cette structure de donnée, il est très aisé de programmer des fonctions de réseaux sociaux basiques.
Par exemple, quels sont les amis de Carole, et de Mallory ?
## Exemple d'usage d'une matrice d'adjacence
## Si la position i vaut 1, alors il y a un lien
utilisateurs = ["Alice","Bob","Carole","David","Eve","Mallory","Oscar","Trudy"]
Alice = [0,1,0,1,0,0,0,0]
Bob = [1,0,1,0,1,0,0,0]
Carole = [0,1,0,0,0,0,1,1]
David = [1,0,0,0,1,1,0,0]
Eve = [0,1,0,1,0,1,1,0]
Mallory = [0,0,0,1,1,0,1,0]
Oscar = [0,0,1,0,1,1,0,1]
Trudy = [0,0,1,0,0,0,1,0]
graphe = [Alice,Carole,David,Eve,Mallory,Oscar,Trudy]
for i in range(len(graphe)):
for j in range(len(graphe)):
if graphe[i][j] != 0 and i != j:
print(utilisateurs[i],"est ami avec",utilisateurs[j])
Alice est ami avec Bob
Alice est ami avec David
Bob est ami avec Oscar
Carole est ami avec Alice
Carole est ami avec Eve
Carole est ami avec Mallory
David est ami avec Bob
David est ami avec Mallory
David est ami avec Oscar
Eve est ami avec David
Eve est ami avec Oscar
Mallory est ami avec Carole
Mallory est ami avec Eve
Oscar est ami avec Carole
Solution des exercices#
Exercice 1#
La matrice d’ajacence est la suivante :
A |
B |
C |
D |
E |
F |
G |
H |
|
|---|---|---|---|---|---|---|---|---|
A |
0 |
3 |
0 |
10 |
0 |
0 |
0 |
0 |
B |
3 |
0 |
12 |
0 |
8 |
0 |
0 |
0 |
C |
0 |
12 |
0 |
0 |
0 |
0 |
7 |
5 |
D |
10 |
0 |
0 |
0 |
4 |
12 |
0 |
0 |
E |
0 |
8 |
0 |
4 |
0 |
2 |
6 |
0 |
F |
0 |
0 |
0 |
12 |
2 |
0 |
4 |
0 |
G |
0 |
0 |
7 |
0 |
6 |
4 |
0 |
15 |
H |
0 |
0 |
5 |
0 |
0 |
0 |
15 |
0 |
