C2-ALGO-04-B : Parcours de graphes

Introduction

Un graphe représente des sommets et des arêtes reliées ou non. Il est facile de représenter un graphe à l’aide d’une matrice d’adjacence.

Le parcours d’un graphe permet de trouver des chemins, c’est-à-dire une suite de sommets reliés entre eux par des arêtes (ou des arcs dans le cas d’un graphe orienté).

Exercice introductif : chemin le plus court 1

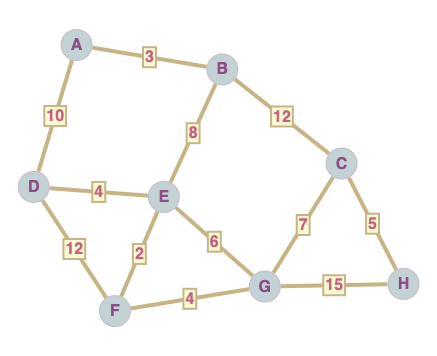
Quel est le chemin le plus court entre les sommets D et H ?

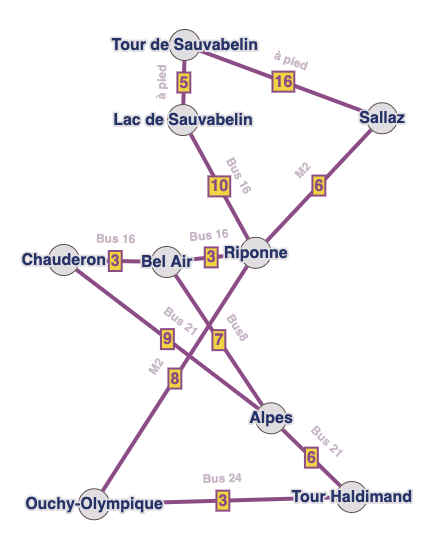
Exercice introductif 2 : chemin le plus cours 2 !

Pour le trajet Tour Haldimand -> Tour de Sauvabelin, Google Maps propose

• Bus 24 jusqu’à Ouchy (3’), M2 jusqu’à Sallaz (14’), puis à pied (16’)

• Bus 21 jusqu’à Alpes (6’), bus 8 jusqu’à Bel Air (7’), bus 16 jusqu’à Sauvabelin (13’), puis à pied (5’)

• Bus 21 jusqu’à Chauderon (18’), bus 16 jusqu’à Sauvabelin(16’), puis à pied (5’)

• 1h15 à pied, ça fait du bien !

• Quel trajet mettrait le moins de temps ?

Faisons le graphe !

Algorithme de Dijkstra

L’algorithme de Dijkstra consiste à partir d’un point (par exemple A) à trouver le chemin le plus court jusqu’à couvrir l’ensemble du graphe.

On ne prend pas deux fois un chemin car on construit un arbre couvrant.

Etapes de l’algorithme de Dijkstra pour trouver le plus cours chemin

1. On initialise les distances : 0 pour le sommet de départ, infini pour les autres.

2. On visite le sommet le plus proche non encore visité.

3. On met à jour les distances pour ses voisins.

4. On répète jusqu’à avoir visité tous les sommets.

L’utilité de la matrice d’adjacence est évidente.

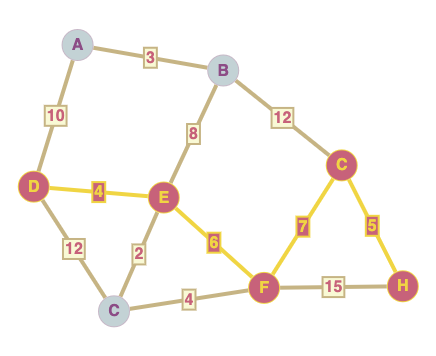
Exemple

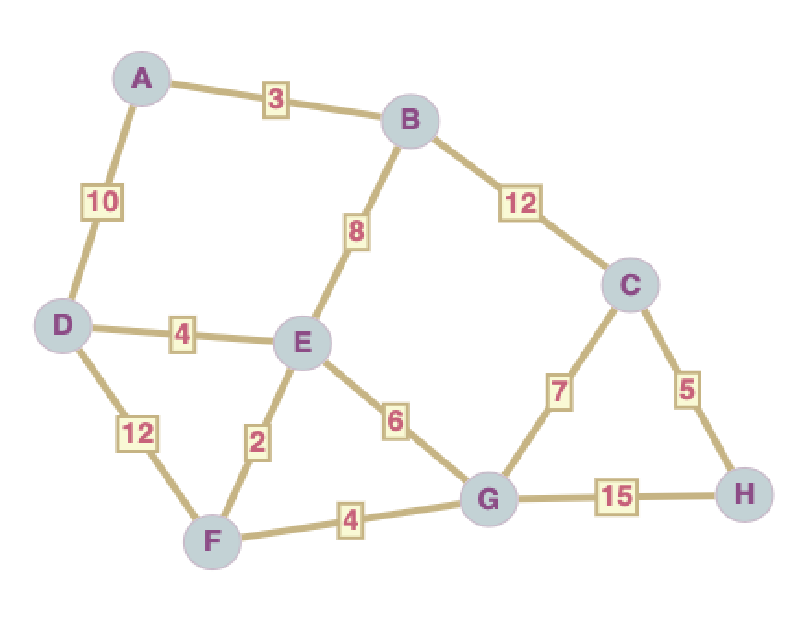
Dans cet exemple, il y a deux chemins qui partent de A et finissent à G de longueur 17 : A-B-E-F-G et A-B-E-G

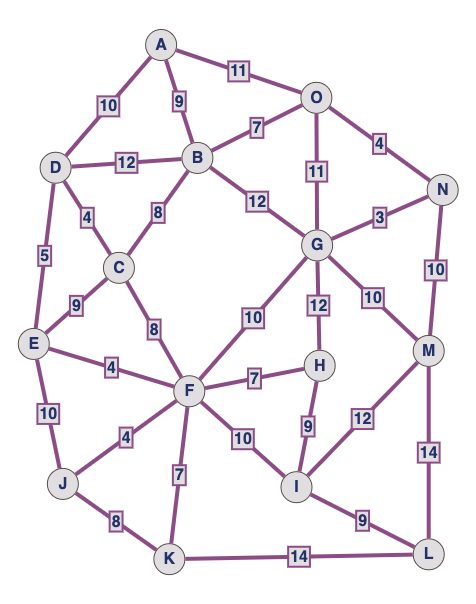
Exercice 1 : Dijkstra

Construire l’arbre recouvrant dans le graphe suivant :

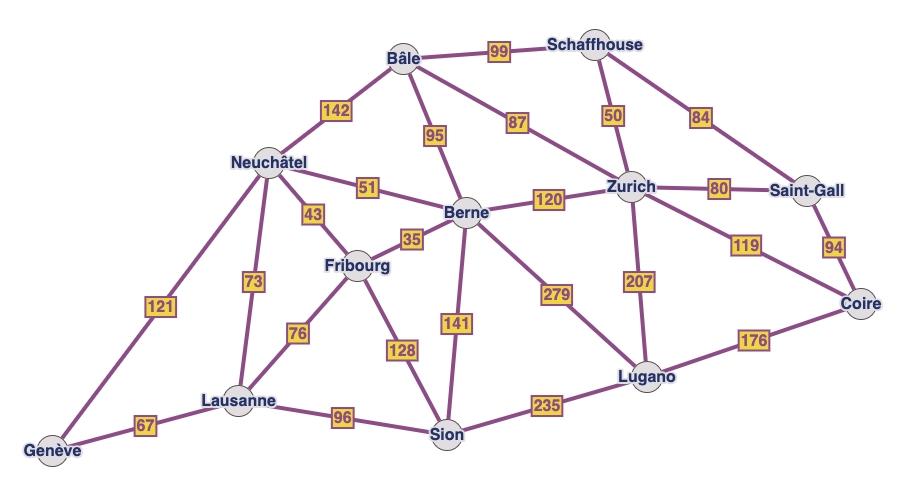
Exercice 2 : Villes suisses

Sur ce graphe, on indique les distances entre quelques villes importantes en Suisse.

Quel est le chemin le plus court entre Genève et Coire ?

## Solution aux exercices

Exercice introductif 1

Voici une solution :

Exercice 2 (villes suisses)

Voici la matrice d’adjacence entre les villes

	Lausanne	Genève	Neuchâtel	Fribourg	Berne	Zürich	Lugano	Sion	Bâle	Schaffhouse	St-Gall	Coire
Lausanne	0	67	73	76	111	231	331	96	206	281	311	350
Genève	67	0	121	143	172	292	398	163	263	342	372	411
Neuchâtel	73	121	0	43	51	171	330	169	142	221	251	290
Fribourg	76	143	43	0	35	155	314	128	130	205	235	274
Berne	111	172	51	35	0	120	279	141	95	170	200	239
Zürich	231	292	171	155	120	0	207	261	87	50	80	119
Lugano	331	398	330	314	279	207	0	235	294	257	270	176
Sion	96	163	169	128	141	261	235	0	246	311	341	380
Bâle	206	263	142	130	95	87	294	236	0	99	167	206
Schaffhouse	281	342	221	205	170	50	257	311	99	0	84	169
St-Gall	311	372	251	235	200	80	270	341	167	84	0	94
Coire	350	411	290	274	239	119	176	380	206	169	94	0

Code Python Dijkstra

Le code suivant permet de calculer la longueur des chemins en utilisant la matrice d’adjacence et l’algorithme de Dijkstra

# Code permettant de calculer l'algorithme de Dijkstra
# sur le graphe du cours C2_ALGO_04
import random

INF = 100000
nbr = 8

A = [ 0, 3, 0,10, 0, 0, 0, 0]
B = [ 3, 0,12, 0, 8, 0, 0, 0]
C = [ 0,12, 0, 0, 0, 0, 7, 5]
D = [10, 0, 0, 0, 4,12, 0, 0]
E = [ 0, 8, 0, 4, 0, 2, 6, 0]
F = [ 0, 0, 0,12, 2, 0, 4, 0]
G = [ 0, 0, 7, 0, 6, 4, 0,15]
H = [ 0, 0, 5, 0, 0, 0,15, 0]


graph = [A,B,C,D,E,F,G,H]

# Nomme le sommet à partir duquel on calcule l'arbre couvrant
premier = 3

noeuds = ["A","B","C","D","E","F","G","H"]

nbr = len(graph)
visites = [False] * nbr
distances = [INF] * nbr
distances[premier] = 0

for i in range(nbr):
    # Recherche des noeuds avec la distance minimum
    min_distance = INF
    min_index = -1
    for v in range(nbr):
        if not visites[v] and distances[v] < min_distance:
            min_distance = distances[v]
            min_index = v

    visites[min_index] = True

    # Recalcul des distances depuis le noeud
    for v in range(nbr):
        if graph[min_index][v] > 0 and not visites[v]:
            new_distance = distances[min_index] + graph[min_index][v]
            if new_distance < distances[v]:
                distances[v] = new_distance

print("Distance depuis la source : ",noeuds[premier])
print("Noeud","\t","Distance")
for i in range(nbr):
    print(noeuds[i],"\t",distances[i])

Distance depuis la source :  D
Noeud 	 Distance
A 	 10
B 	 12
C 	 17
D 	 0
E 	 4
F 	 6
G 	 10
H 	 22