
C1-ALGO-14 : Algorithmes évolutionnistes#
Objectifs pédagogiques#
Comprendre que l’évolution naturelle est un processus algorithmique
Identifier les différentes briques d’un algorithme génétque
Introduction : la couleur des yeux#
Est-ce que la couleur des yeux des enfants peut-être prédite en regardant la couleur des yeux des parents ?
Est-ce que la couleur des yeux c’est du HASARD ?
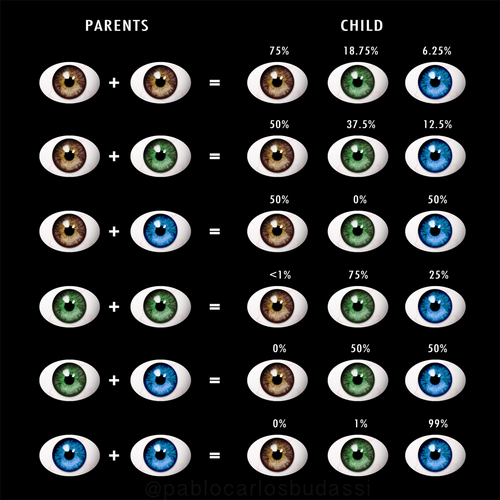
source de l’image : wikimedia
Si ce n’est pas du hasard, alors cela vient d’où ?
Génétique#
La génétique est la science qui s’occupe des lois de l’hérédité. C’est un sujet majeur pour comprendre comment se transmettent les caractéristiques des individus d’une espèce d’une génération à la suivante, mais aussi de manière globale sur la population.
Charles Darwin propose le concept de sélection naturelle par opposition à sélection artificielle pratiquée depuis des millénaires par l’Être Humain : la sélection des individus possèdant les meilleures caractéristiques pour la population suivante.
Définition#
Les algorithmes évolutionnistes sont une classe d’algorithmes qui s’inspirent de la théorie de l’évolution de Charles Darwin. Cette classe d’algorithmes utilise des processus qui imitent le vivant, notamment les trois grands mécanismes de la reproduction sexuée des êtres vivants :
la reproduction : on mélange des caractéristiques
la mutation : certaines caractéristiques changent aléatoirement
la sélection : les meilleurs individus survivent (il faut définir meilleur)
Selon la théorie de l’évolution, sur une population donnée d’individus tous différents, ceux qui ont unt chance de transmettre leurs caractéristiques sont ceux qui sont les mieux adaptés à leur environnement.
En algorithmique évolutionniste, un individu est une solution possible.
La très grande difficulté de ces algorithmes est la capacité que doit avoir le processus pour évaluer la qualité d’une solution. Cela se fait grâce à une fonction d’objectif (fitness function en anglais)
Peut-on faire “évoluer” un programme vers une solution ?#
Voici un exemple. Nous souhaitons qu’un programme retrouve un mot choisi. Par exemple BONJOUR. Mais le programme:
n’est pas une IA
n’a accès à aucune base de donnée (dictionnaire ou autre)
n’a aucune connaissance a prior de la grammaire française
doit pouvoir être écrit par un gymnasien de première année
Quelle stratégie ?
Tout tester au hasard ? En utilisant seulement les lettres majuscules. Le mot BONJOUR contient 7 lettres, le nombre total de possibilités atteint \(26^{7} = 7836416496\) soit environ \(7^{9}\). Si un ordinateur peut tester un milliard de solutions par secondes, cela équivaut à y passer plus de 8 secondes. Dans le monde des pirates informatiques, on appelle cela une attaque en force brute
Utiliser une approche évolutionniste. A chaque essai, on garde les morceaux de phrases qui ressemblent le plus à la cible, puis on les mélange, puis on les combine. Exactement comme fait la nature.
Algorithmes évolutionnistes#
il existe plusieurs classes d’algorithmes évolutionnistes
les stratégies d’évolution
les algorithmes génétiques
Algorithmes génétiques#
Les algorithmes génétiques s’inspirent des mécanismes de la génétique et particulièrement ceux liés à l’Acide désoxyribonucléique (ADN). La théorie de l’évolution considère que la majorité des caractéristiques d’un être vivant est contenue dans la double hélice de l’ADN.
Voici un algorigramme d’un algorithme génétique :
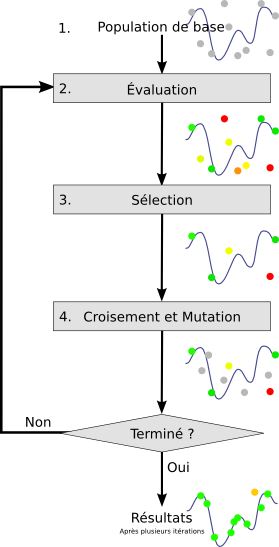
Population de base (initiale)#
Création de la population initiale. Chaque individu de cette population est une solution possible.
La génération de cette population initiale peut se faire par différentes techniques :
Aléatoirement
avantage : grande diversité
inconvénient : risque de lenteur au démarrage de l’algorithme
Aléatoirement mais avec des contraintes sur les individus (par exemple, les individus doivent respecter des règles de base)
avantage : élimine les solutions invalides dès le départ
Semi-aléatoirement. A l’aide d’un autre algorithme, on génère des individus de bonne qualité
avantage : démarrage plus rapide de l’algorithme
inconvénient : risque de réduction de la diversité
Solution hybride. Une partie de la population initiale est faite avec les méthodes (1), (2) ou (3)
De manière générale, la taille de la population initiale doit être suffisamment grande pour assurer de la diversité dans les solutions possibles, mais pas trop pour conserver une certaine efficacité.
Evaluation#
Pour évaluer une solution, on s’intéresse à la qualité de cette solution par rapport à la cible recherchée.
En algorithmique génétique, on dit que l’on calcule la fonction de fitness de la solution. C’est-à-dire une valeur numérique représentant la qualité de la solution.
Exemple : un test d’informatique est passé par une classe. Chaque élève propose une solution (les exercices du test). La fonction de fitness est alors la note reçue par l’élève.
Sélection#
Une fois l’évaluation faite sur tous les individus, il s’agit de sélectionner quels sont ceux qui feront partie des parents de la prochaine génération. L’idée ici n’est pas de garder uniquement les meilleurs, mais de leur donner plus de chances d’être choisis. Cela permet de garder de la diversité mais de favoriser les bonnes solutions.
Ici on sélectionne les différents individus. Il existe plusieurs méthodes pour sélectionner un individu parmi deux :
la roulette (le hasard pur)
la roulette biaisée
Un tournoi entre les deux
l’élitisme (on sélectionne que le meilleur)
Un mixe
Croisements et mutations#
Une fois les parents sélectionnés, on peut créer la génération suivante. Pour faire cela, on s’inspire de la nature. Deux parents font des enfants en associant leurs gènes et parfois, cette opération est modifiée par une mutation.
croisement : il s’agit de combiner les bonnes caractéristiques des deux parents pour créer un ou plusieurs enfants. Une partie du gène de l’individu 1 est combiné à la seconde partie de l’individu 2. La limite est appelée point de coupure. Il en résulte deux individus.
mutation : introduction de modification du gène de l’enfant. Au hasard
Algorithme génétique simple : le mot secret#
A l’aide d’un algorithme génétique, nous allons retrouver un mot secret. Le mot secret est un mot de 7 lettres en majuscules et il est connu que du seul prof.
Principe :#
Chaque élève :
reçoit quatre mots de 7 lettres au hasard. C’est la population initiale (ou génération 0)
évalue le fitness de ses mots. Seuls deux seront conservés. Avec la population initiale, les deux sont choisi automatiquement. C’est la phase de sélection naturelle. Seuls les meilleurs sont choisis.
croise ses deux mots. C’est la phase de reproduction. Le point de coupure (crossover point) est choisi au hasard avec un dé à jouer
mute ou non un gène des deux enfants. C’est la phase de mutation.
Il y a mutation si la valeur d’un dé tiré est de 1, aucune mutation sinon
Le point de mutation et la nouvelle valeur de lettre seront choisis au hasard avec les dés.
L’algorithme reprend au point 2.
Faire évoluer votre population jusqu’à la génération 4
Annexes#
Codage des lettres (codons) avec deux dé à jouer#
On va utiliser deux dés à 6 faces de couleurs différentes pour coder les 26 lettres de l’alphabet (uniquement les majuscules). Sur les 36 possibilités, 10 ne seront pas utilisées. Si ces 10 combinaisons tombent, alors on relance les deux dés
dé 1 (blanc) |
dé 2 (ivoire) |
Lettre |
|---|---|---|
1 |
1 |
A |
1 |
2 |
B |
1 |
3 |
C |
1 |
4 |
D |
1 |
5 |
E |
1 |
6 |
F |
2 |
1 |
G |
2 |
2 |
H |
2 |
3 |
I |
2 |
4 |
J |
2 |
5 |
K |
2 |
6 |
L |
3 |
1 |
M |
3 |
2 |
N |
3 |
3 |
O |
3 |
4 |
P |
3 |
5 |
Q |
3 |
6 |
R |
4 |
1 |
S |
4 |
2 |
T |
4 |
3 |
U |
4 |
4 |
V |
4 |
5 |
W |
4 |
6 |
X |
5 |
1 |
Y |
5 |
2 |
Z |
Générateur de mots aléatoires de 7 lettres majuscules#
# -------------------------------------------------------------
# Générateur de mots aléatoires de 7 lettres
# Vincent Keller (c) 2026
# -------------------------------------------------------------
import random
alphabet = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
nombre = 10
i = 0
while i < nombre:
j = 0
mot = ""
while j < 7:
pos = random.randint(1,26)
mot = mot + alphabet[pos-1]
j = j + 1
print(mot)
i = i + 1
JBNIBXA
BOAEOMD
IWIPYAK
QQDSMXW
NRWXKJG
MBSBLRT
LBFLXMR
HAREMVG
EJMICEC
KOTAHMF
Code python complet#
Attention, ce code n’est pas le plus optimal dans son écriture. Il mobilise les concepts de programmation vus au cours (boucles, tests conditionnels, variables, listes, etc..)
# -------------------------------------------------------------
# Générateur de mots aléatoires de X lettres (x est la longueur)
# Vincent Keller, Gymnase de Beaulieu, (c) 2026
# -------------------------------------------------------------
import random
longueur = 7
taille_population = 100 # Doit être pair !
generations = 30
taux_mutation = 1 # Compris entre 1 et 6 (dé à jouer)
alphabet = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
def init_individu():
j = 0
mot = ""
while j < longueur:
pos = random.randint(1,26)
mot = mot + alphabet[pos-1]
j = j + 1
return mot
def fitness(individu,cible):
i = 0
fit = 0
while i < len(individu):
if individu[i] == cible[i]:
fit = fit + 1
i = i + 1
return fit
def selection(pop,cible):
i = 0
fit_pop = []
sel_pop = []
while i < len(pop):
ind = [pop[i],fitness(pop[i],cible)]
fit_pop.append(ind)
i = i + 1
i = 0
# Tri de la liste en fonction des fitness
fit_pop = sorted(fit_pop,key=lambda x: x[1])
i = taille_population - 1
while i >= 0:
sel_pop.append(fit_pop[i][0])
i = i - 1
# Renvoi d'une liste de taille taille_population (les taille_population plus forts)
return sel_pop
def crossover(ind1,ind2):
new_ind1 = ""
new_ind2 = ""
i = 0
# Point de mutation (pour le jeu, 1 à 6 fonctionne)
point = random.randint(1,longueur)
while i < len(ind1):
if i < point:
new_ind1 = new_ind1 + ind1[i]
new_ind2 = new_ind2 + ind2[i]
else:
new_ind1 = new_ind1 + ind2[i]
new_ind2 = new_ind2 + ind1[i]
i = i + 1
return new_ind1, new_ind2
def mutation(ind):
point = random.randint(1,longueur)
new_ind = ""
i = 0
while i < longueur:
if i == point:
pos = random.randint(1,26)
new_ind = new_ind + alphabet[pos-1]
else:
new_ind = new_ind + ind[i]
i = i + 1
return new_ind
## INITIALISATION
population = []
i = 0
while i < taille_population:
population.append(init_individu())
i = i + 1
secret = input("Quel mot à rechercher : ")
secret = secret.upper()
#variable permettant de savoir si l'algorithme a convergé
trouve = False
## GENERATIONS
g = 0
while g < generations:
## SELECTION
sel = selection(population, secret)
fit_max = 0
## CROSSOVER
i = 0
while i < taille_population:
ind1, ind2 = crossover(sel[i], sel[i+1])
sel[i] = ind1
sel[i + 1] = ind2
i = i + 2
## MUTATION
i = 0
while i < taille_population:
mut = random.randint(1,6)
if mut < taux_mutation :
sel[i] = mutation(sel[i])
i = i + 1
# A-T-ON TROUVE LE SECRET ?
i = 0
while i < taille_population:
fit = fitness(sel[i], secret)
#print(sel[i],fit)
if fit == longueur:
print("Mot secret trouvé : ",sel[i],"à la génération",g)
# permet de sortir de la boucle
trouve = True
g = generations + 1
i = taille_population + 1
i = i + 1
## RECOPIE DE LA POP SEL VERS LA POPULATION
population.clear()
population = sel.copy()
sel.clear()
g = g + 1
if trouve == False:
print("L'algorithme n'a pas trouvé de solution")
---------------------------------------------------------------------------
StdinNotImplementedError Traceback (most recent call last)
Cell In[2], line 85
82 population.append(init_individu())
83 i = i + 1
---> 85 secret = input("Quel mot à rechercher : ")
86 secret = secret.upper()
88 #variable permettant de savoir si l'algorithme a convergé
File ~/.local/pipx/venvs/jupyter-book/lib/python3.11/site-packages/ipykernel/kernelbase.py:1274, in Kernel.raw_input(self, prompt)
1272 if not self._allow_stdin:
1273 msg = "raw_input was called, but this frontend does not support input requests."
-> 1274 raise StdinNotImplementedError(msg)
1275 return self._input_request(
1276 str(prompt),
1277 self._parent_ident["shell"],
1278 self.get_parent("shell"),
1279 password=False,
1280 )
StdinNotImplementedError: raw_input was called, but this frontend does not support input requests.
Références#
Charles Darwin, On the Origin of Species by Means of Natural Selection}, 1859 : [Darwin, 1859]
David Goldberg, Genetic Algorithms in Search, Optimization, and Machine Learning , 1989 : [Goldberg, 1989]
homas Vallée, Murat Yildizoglu, Présentation des algorithmes génétiques et de leurs applications en économie, 2004, [Thomas Vallée, 2004]
