
C2-ALGO-01 : Taille du problème#
Objectifs pédagogiques#
Identifier la ou les variables qui représentent la variation de taille d’entrée de l’algorithme sur quelques algorithmes classiques
déduire la complexité temporelle de l’algorithme
Taille d’entrée d’un algorithme#
Parmi les différentes caractéristiques d’un algorithme, on rappelle qu’un algorithme a:
un algorithme a des entrées, zéro ou plus, quantités qui lui sont données avant ou pendant son exécution
S’il y a une entrée ou plus, cela signifie que la taille peut être connue avant l’exécution de l’algorithme.
Quelques exemples d’entrées :
une liste de taille
len(maListe): par exemple dans le cas d’un algorithme de recherche ou de triun périmètre (
range) entre une borne inférieureborneInfet une borne supérieureborneSup: par exemple dans le cas d’un algorithme du type Fibonacci où l’on calcule explicitement une suite de nombres en fonction d’un paramètre de boucle
Analyse de la taille#
Une fois l’entrée ou les entrées de l’algorithme identifiées, il s’agit d’analyser comment celles-ci font varier le nombre d’opérations ou d’instructions N.
Formellement, on ajoute une boucle externe dont l’itérateur (la variable itérateur) de la boucle devient la variable d’entrée. Cette boucle permet de monitorer le code : mesurer le nombre d’opérations N en fonction de la taille de l’entrée
Voici comment on le représente avec un algorigramme :
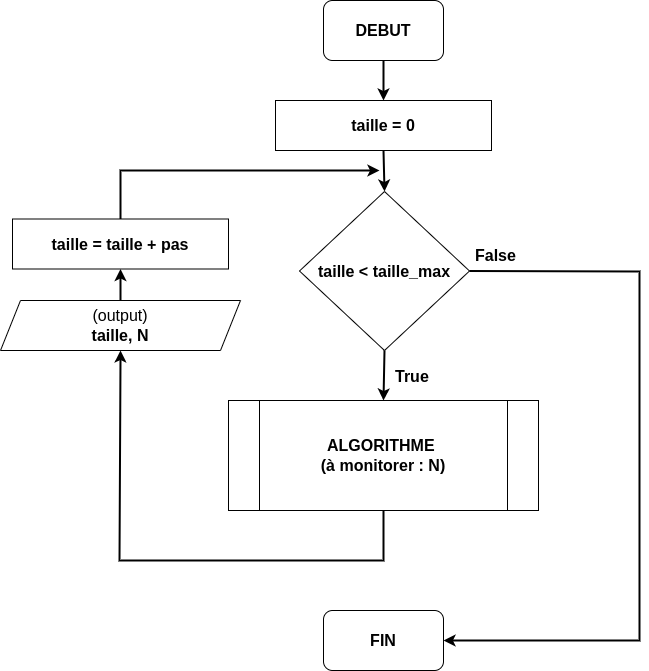
Cela permet, lorsqu’on analyse N en fonction de la taille de déduire quelle est la complexité. Cela se fait avec un tableau qui liste la taille de l’entrée et le nombre d’opérations ou d’instructions :
|
|
|---|---|
0 |
0 |
500 |
64 |
1000 |
128 |
1500 |
256 |
2000 |
512 |
2500 |
1024 |
3000 |
2048 |
3500 |
4096 |
4000 |
8192 |
Exercice 1#
quelle taille de l’entrée avant exécution ?
peut-elle varier ?
quelle est la complexité de l’algorithme ?
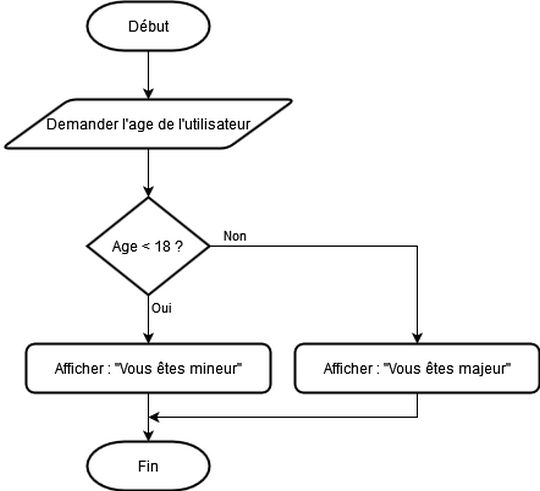
Exercice 2#
quelle taille de l’entrée avant exécution ?
peut-elle varier ?
quelle est la complexité de l’algorithme ?
## Insertion sort example
import random
nombres = []
longueur = 10
## Remplissage de la liste
for i in range(longueur):
aleat = random.randint(0,longueur)
nombres.append(aleat)
print(nombres)
## Insertion sort itself
j = 1
while j <= longueur-1:
i = j - 1
k = nombres[j]
while i >= 0 and nombres[i] > k:
nombres[i+1] = nombres[i]
i = i - 1
nombres[i+1] = k
j = j + 1
print(nombres)
[10, 6, 6, 4, 3, 6, 6, 10, 10, 5]
[3, 4, 5, 6, 6, 6, 6, 10, 10, 10]
Exercice 3#
quelle taille de l’entrée avant exécution ?
peut-elle varier ?
quelle est la complexité de l’algorithme ?
# Recherche aléatoire avec remise dans une liste triée commentée
# Vincent Keller, 2023
# Importation de la bibliothèque random (nombres aléatoires)
import random
# Input borneInf
borneInf = 0
# Input borneSup
borneSup = 100
# variable atrouver : nombre aléatoire de type entier compris entre borneInf et borneSup (compris)
atrouver = random.randint(borneInf,borneSup)
# N est la variable qui contiendra le nombre de comparaisons
N = 0
# trouve est une variable de type booléen.
trouve = False
# Boucle "tant que la variable trouve n'est pas égale à True)
while (trouve!=True):
# On tire un nombre que l'on assigne à la variable aleatoire
aleatoire = random.randint(borneInf,borneSup)
# Si le nombre à trouver est égal au nombre aléatoire tiré, alors on sort de la boucle
if (aleatoire == atrouver) :
trouve=True
# On incrémente le nombre de comparaisons
N = N + 1
# Output : affichage du nombre à trouver et du nombre de comparaisons
print("Nombre d'opérations pour trouver "+str(atrouver)+" : "+str(N))
Nombre d'opérations pour trouver 35 : 11
Exercice 4#
quelle taille de l’entrée avant exécution ?
peut-elle varier ?
quelle est la complexité de l’algorithme ?
annee = 2023
if (annee%4 != 0) :
print(str(annee)+" n'est pas une année bisextile")
else:
if (annee%100 != 0) :
if (annee%400 != 0) :
print(str(annee)+" est une année bisextile")
else:
print(str(annee)+" n'est pas une année bisextile")
else:
print(str(annee)+" est une année bisextile")
2023 n'est pas une année bisextile
Exercice 5#
quelle taille de l’entrée avant exécution ?
peut-elle varier ?
quelle est la complexité de l’algorithme ?
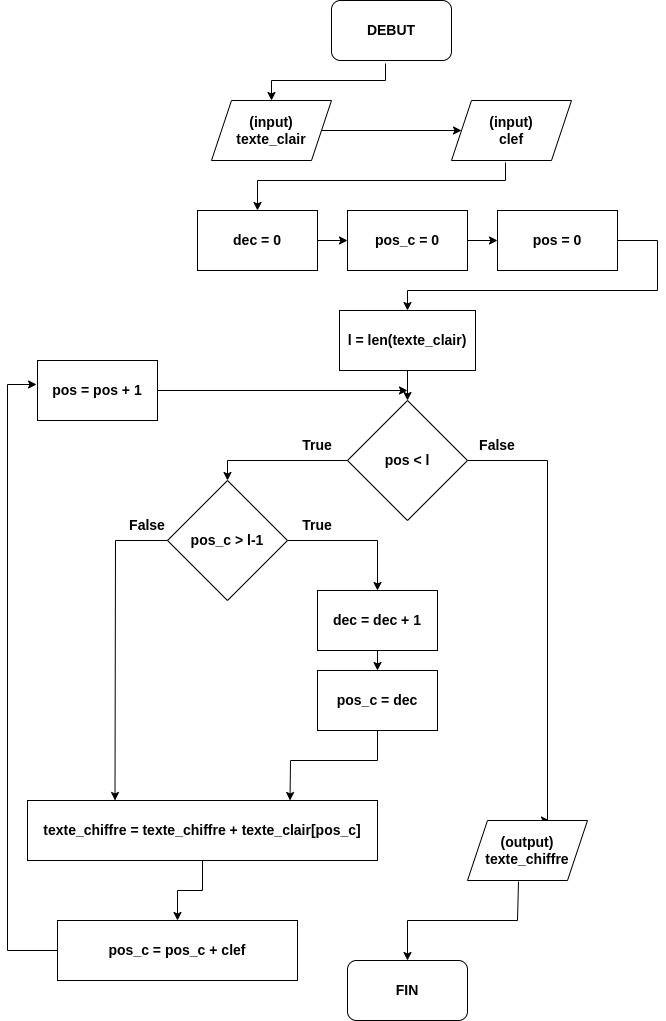
Correction des exercices#
Exercice 1#
Vérification de l’âge d’un client dans une piscine
Quelle taille de l’entrée avant exécution ?#
La taille de l’entrée est constante : l’âge demandé
Peut-elle varier ?#
Non, elle ne varie pas
Quelle est la complexité de l’algorithme ?#
C’est un algorithme de classe de complexité constante : \(\mathcal O (1)\)
Exercice 2#
Tri d’une liste de nombres aléatoires avec le tri par insertion
Quelle taille de l’entrée avant exécution ?#
C’est la longueur de la liste de nombres à trier : longueur. Ici la valeur est 10
Peut-elle varier ?#
Oui elle peut varier.
Quelle est la complexité de l’algorithme ?#
Deux boucles imbriquées signifie que c’est une classe de complexité quadratique : \(\mathcal O (N^2)\)
Exercice 3#
Recherche d’un élément dans une liste triée en utilisant l’algorithme de recherche aléatoire avec remise du nombre tiré : l’algorithme est susceptible de reprendre le même nombre trié autant de fois qu’il le souhaite.
Quelle taille de l’entrée avant exécution ?#
C’est la longueur de la liste triée : borneSup - borneInf. Ici la valeur est 100
Peut-elle varier ?#
Oui elle peut varier
Quelle est la complexité de l’algorithme ?#
Si la liste est formée de nombres vraiment aléatoires, alors la complexité algorithmique dans le pire des cas n’est pas définie. Ce programme n’implémente pas un algorithme puisque, par définition, un algorithme doit avoir une fin.
Exercice 4#
Une année entrée en paramètre est-elle bissextile ou pas ?
Quelle taille de l’entrée avant exécution ?#
La taille de l’entrée est constante : c’est la valeur de l’année entrée par l’utilisateur.
Peut-elle varier ?#
Non, il s’agit toujours d’un entier qui représente une année.
Quelle est la complexité de l’algorithme ?#
C’est un algorithme de classe de complexité constante : \(\mathcal O (1)\)
Exercice 5#
Chiffrement d’un texte clair en utilisant l’algorithme par décalage (algorithme de Jules César)
Quelle taille de l’entrée avant exécution ?#
Il s’agit de la longueur du texte clair à chiffrer : l = len(texte_clair)
Peut-elle varier ?#
Oui elle peut varier.
Quelle est la complexité de l’algorithme ?#
Pour chaque lettre du texte clair, l’algorithme calcule la lettre chiffrée. Il s’agit donc d’une boucle simple. La classe de complexité algorithmique est donc linéraire : \(\mathcal O (N)\)
