
C1-REDO-04 : codage de caractères#
Objectifs pédagogiques:#
Comprendre la représentation numérique des caractères
Comprendre qu’il faut se mettre d’accord sur un alphabet commun
Appliquer sur une communication réussie dans l’aviation
Comprendre et appliquer le codage ASCII
Déduire l’alphabet UniCODE de l’alphabet ASCII
Introduction#
Un fichier informatique n’est finalement rien d’autre qu’une suite d’octets. Historiquement, il a fallu trouver une convention afin que les différents ordinateurs qui ont commencé à communiquer puissent s’entendre.
Questions#
Questions🔌
1 - qu’est-ce qu’on écoute ?
Réponse
2 - Que disent-ils ?
Réponse
3 - Y a-t-il des mots qui arrivent souvent ?
Réponse
4 - Comment les intervenants se comprennent-ils ?
Réponse
Il y a un indicatif de l’émetteur, un indicatif du récepteur, un alphabet commun, des métriques communes
Exemple introductif : alphabet de l’aviation#
L’alphabet radiophonique international est utilisé pour transmettre des messages quelque soit les possibles interférences, incompréhensions entre locuteurs ou mode de transmission.
Il consiste à transmettre un mot acrophonique, c’est-à-dire dont la première lettre représente la lettre transmise.
Voici le code de l’OACI (Organisation de l’Aviation Civile Internationale) :

Chaque code a été réfléchi afin que si une partie seulement de celui-ci est transmise, il soit possible de comprendre l’entier du message.
Utilisation#
Indicatif de l’émetteur
Indicatif du récepteur
Message
Fin
Exemples
L’avion long-courrier immatriculé PT-FSB est autorisé au décollage
…Fox-trot Sierra Bravo, heavy, runway two-two, clearance allowed, wind three-ten-zero, eight knots
Il existe des situations où toute communication est levée : l’urgence absolue. Exemple, l’avion immatriculé HB-CDF demande l’urgence absolue :
… Mayday, mayday, mayday, Hotel, Bravo, Charlie, Delta, Fox, mayday, mayday, mayday. Fire on board. Request to land immediately
Exercice : transmettre un message#
Transmettez par oral votre prénom en utilisant l’alphabet de l’OACI
Exercice : transmettre un message partiellement#
Simulez un problème de communication et transmettez votre prénom par oral en utilisant que la moitié du mot de l’alphabet de l’OACI
Communication entre ordinateurs#
Dans un réseau, comme Internet, deux ordinateurs doivent aussi “se mettre d’accord” pour communiquer dans de bonnes conditions.
Historiquement, c’est du texte qui a été transmis entre deux ordinateurs pour la première fois.
Il s’agit notamment d’établir un code pour qu’une lettre envoyée soit décodée correctement par le récepteur.
Le codage ASCII#
Le code ASCII pour American Standard Code for Information Interchange est né dans les années 1960 aux USA. La table est basée sur un encodage sur 7 bits.
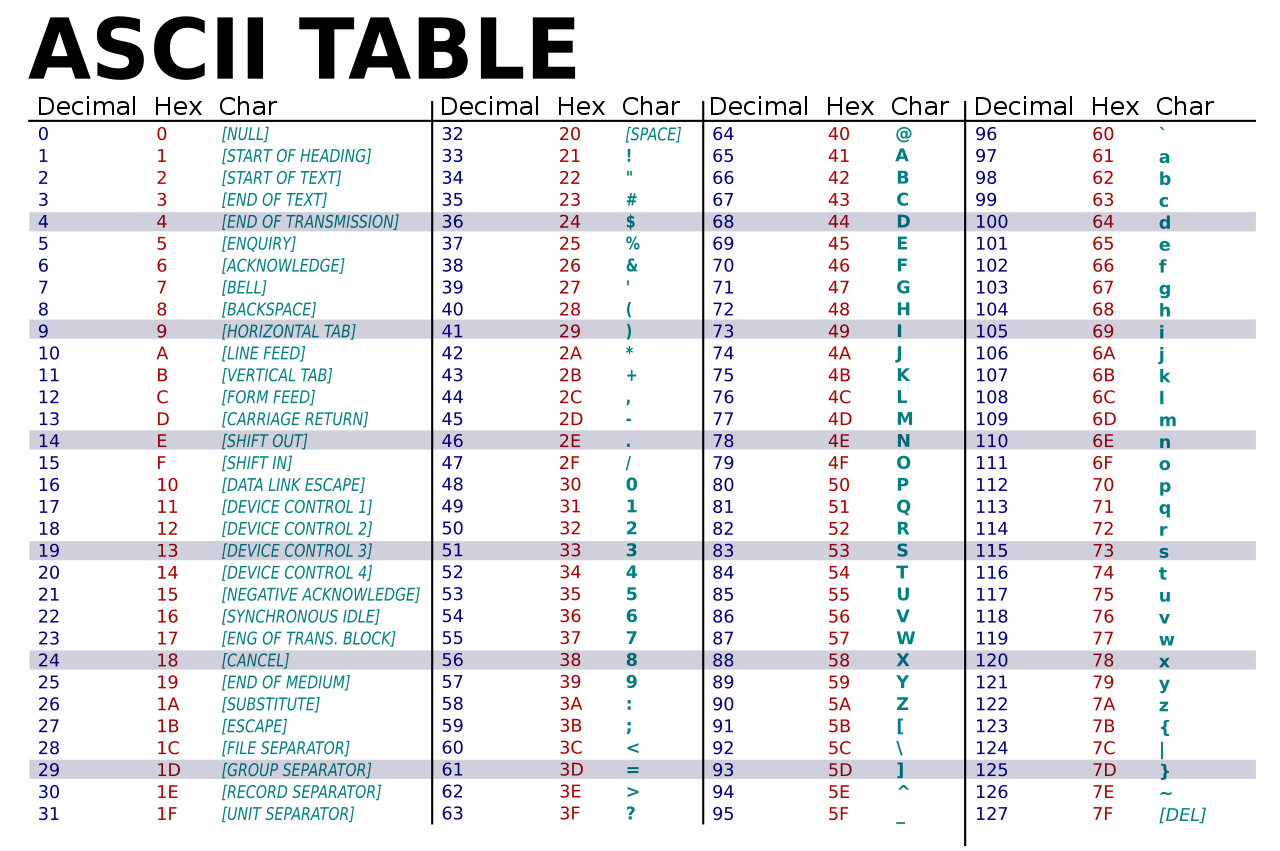
Définition : nombre entier hexadécimal#
Un nombre entier hexadécimal est un nombre entier qui s’écrit uniquement avec les seize symboles 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E et F
Conversion d’un nombre entier binaire en hexadécimal (base 2 à base 16)#
Il suffit de regrouper les bits par paquets de 4, quitte à rajouter des 0 sur les bits de poids fort (à gauche)
Exemple :
\(101001000011_{2}\) en base 2
\(1010_{2} , 0100_{2}, 0011_{2}\) toujours en base 2
\(1010_{2} = A_{16}\), \(0100_{2} = 4_{16}\), \(0011_{2} = 3_{16}\)
En base 16 : A43
Exercice 1#
Ecrivez le code binaire pour les caractères suivants :
A
a
0
Exercice 2#
Quel est le texte encodé par les caractères suivants :
\(42_{16}, 6F_{16}, 6E_{16}, 6A_{16}, 6F_{16}, 75_{16}, 72_{16}\)
\(1000010_{2}, 1001001_{2}, 1100101_{2}, 1101110_{2}, 1110110_{2}, 1100101_{2}, 1101110_{2}, 1110101_{2}, 1100101_{2}\)
\(49_{10}, 57_{10}, 55_{10}, 53_{10}\)
ASCII Art#
Dans les jeunes années de l’informatique, il a été trouvé des moyens de communiquer des images sous la forme d’arrangements des symboles de l’alphabet ASCII. C’est ce que on appelle ASCII Art
Exercice 3 (pour aller plus loin)#
Comment faire la différence entre un octet qui représente un nombre entier et un octet qui représente un encodage en ASCII (pour autant que le bit de poid le plus fort soit mis à 0) ?
Le codage Unicode#
Le codage ASCII ne permet pas d’écrire des caractères accentués ou des symboles provenant d’autres langues. C’est par exemple le cas du chinois, de l’arabe ou du grec mais aussi les hiéroglyphes égyptiens ou les émojis par exemple.
Pour ce faire, il a fallu étendre le codage à plus de bits. Unicode est le standard le plus accepté. Il est possible de coder des caractères en utilisant 32 bits au maximum.
Cela signifie qu’il est possible de coder \(2^{32}\) caractères différents, soit plus de 4 milliards (4’294’967’296) ce qui devrait suffir pour les besoins actuels et futurs de l’ensemble des codages de la planète.
